A Hessian-based assessment of atomic forces for training machine learning interatomic potentials

https://doi.org/10.1063/5.0082952

При моделировании, ab inito расчеты свойств интересующей системы нередко слишком дороги из-за ее размера. По этой причине встает задача о выборе репрезентативной подсистемы, размер которой делал бы доступным ab initio расчеты, и одновременно позволял бы воспроизводить свойства полной системы. Эта проблема актуальна и при обучении потенциалов.

В статье представлен метод определения такой достаточно малой, но репрезентативной подсистемы на основе анализа Гессиана.

Считается хорошей практикой при подготовке обучающей выборки для потенциала проверять сходимость сил и энергий не только относительно параметров первопринципных методов (таких как плотность сетки k-точек или полнота электронного базиса), но и относительно размера конфигурации.

Подчеркивается, что достижение сходимости по силам нужно проверять отдельно, и не ограничиваться только достижением сходимости по энергии, поскольку силы являются менее локальным свойством. Например, для воспроизведения зависимости энергии атома от его окружения, необходимо знать информацию о его соседях в пределах некоторого радиуса отсечки, тогда как для воспроизведения сил на этом атоме, необходимо включить информацию о соседях внутри вдвое большего радиуса.

В данном случае упомянутый радиус отсечки напрямую соответствует гиперпараметру потенциала, выбираемому пользователем для каждой конкретной системы.

Для определения оптимального радиуса отсечки делают “тесты на локальность” (locality tests). Ранее в литературе был описан тест, подразумевающий исследование сходимости по силе на центральном атоме конфигурации в зависимости от радиуса отсечки, за которым атомы испытывают случайные (или смоделированные молекулярной динамикой) смещения. Такой тест требует обсчетов некоторого числа репрезентативных конфигураций при каждом выбранном значении радиуса отсечки, и является довольно вычислительно затратным. 

Предлагаемый в данной работе метод требует расчет только для одной конфигурации, однако для нее требуется построение Гессиана. Из матрицы Гессе можно получить информацию о зависимости сил на каждом из атомов от смещений его соседей. Тест применяется для определения размера подсистемы, в которой силы были бы близки к силам в полной системе. Например, так можно определить размер ячейки, необходимой для точного моделирования периодической системы; или размер молекулярного кластера, который можно будет использовать вместо моделирования жидкости; или репрезентативный фрагмент большой молекулы.

Предлагаемый тест обладает несколькими преимуществами перед описанным ранее в литературе:

1. возможность получить информацию о силах на всех атомах в зависимости от смещений соседей каждого из них, тогда как предложенный ранее тест опирался только на информацию о центральном атоме
2. не нужно делать несколько расчетов со случайными смещениями за радиусом отсечки, беспокоиться о репрезентативности смещенных конфигураций
3. в некоторых случаях возможно взаимное компенсирование сил на атомах в силу симметрии системы, и этот эффект будет затруднительно увидеть из предложенного ранее теста, но по предлагаемому тесту с Гессианом это информация будет доступна из анализа матрицы

Авторы вводят определение матрицы Гессе через ее матричный элемент:

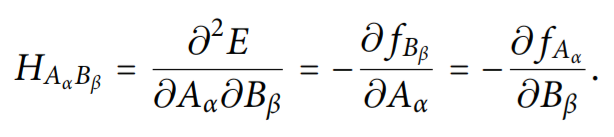
где A и B - это атомы, alpha и beta - xyz компоненты.

Тогда взаимодействие выбранной пары атомов будет соответствовать подматрице Гессиана:

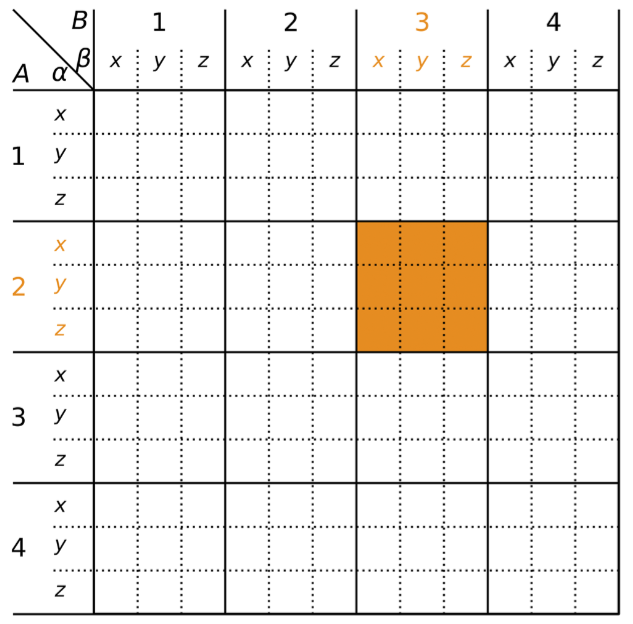
Это взаимодействие между парой атомов можно будет характеризовать скалярной величиной:

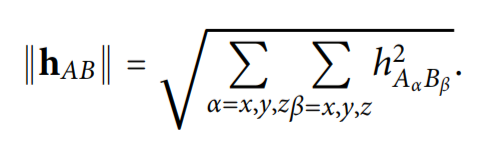
где h_{A_alpha B_beta} – это элементы выбранной подматрицы.

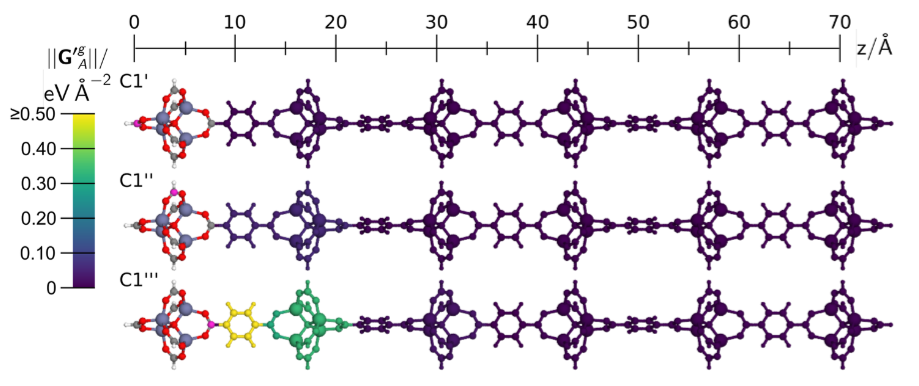
Например, если интересующая система – большая молекула, которую у нас нет возможности моделировать целиком, и стоит задача выбрать репрезентативный фрагмент, где взаимодействие интересующего атома с соседями за пределами фрагмента было бы пренебрежимо мало, то введенная величина ||h_AB|| позволит получить именно эту информацию, что было сделано авторами для нескольких органических молекул:

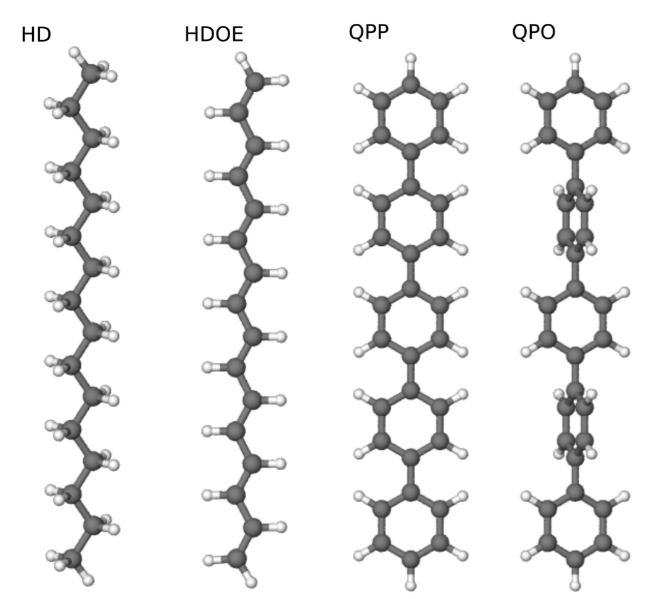
Для них были рассчитаны значения ||h_AB|| для взаимодействия выбранного атома со всеми остальными:

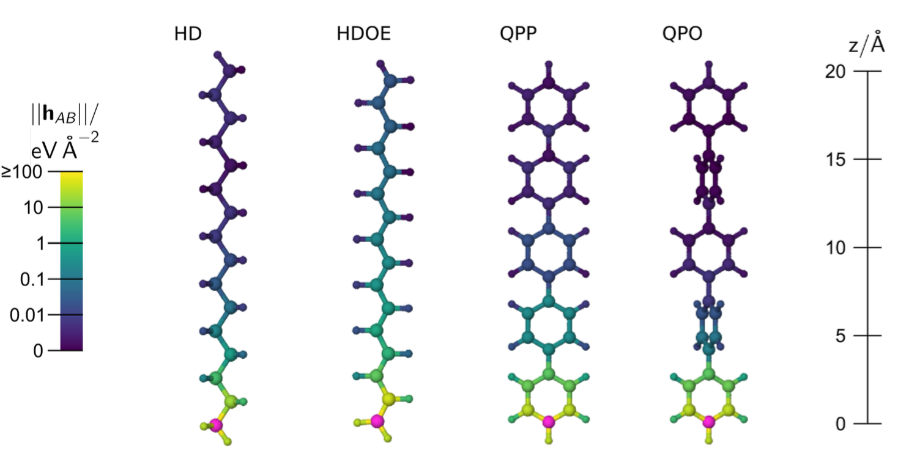
Однако, бывает необходимо выделить подгруппы атомов в молекуле, отвечающие какому-либо функциональному фрагменту: например, функциональной группе или звену полимера. Такое выделение позволит более грамотно подойти к определению фрагмента большой молекулы, который был бы репрезентативен.

Для этого можно ввести величину, охарактеризовавшую бы силу взаимодействия между интересующим атомом с соседями, не присутствующими в рассматриваемом фрагменте, но присутствующими в полной молекуле:

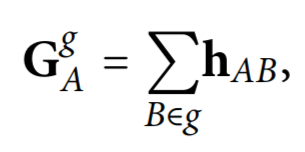
где h_AB - подматрица полного Гессиана, отвечающая взаимодействию между выбранным атомом А и соседом В, и суммирование идет по соседям, не входящим в рассматриваемый фрагмент полной системы.

Поскольку при выделении фрагмента из полной молекулы, неизбежно будет необходимо разорвать некоторое количество химических связей, что приведет к перестройке электронной структуры молекулы, авторы предлагают заменить все обрезанные фрагменты большой молекулы на атомы водорода. Эти изменения также будет необходимо учесть в матрице G_A^g:

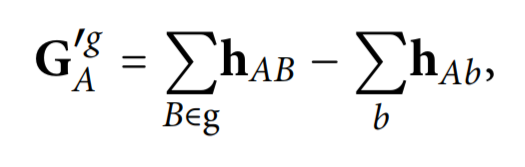
где h_Ab - добавленные подматрицы, отвечающие взаимодействию выбранного атома с добавленными атомами водорода.

Для G_A^’g также можно ввести скалярную характеристику ||G_A^’g|| по аналогии с тем как это было сделано для пары атомов, но теперь такая величина будет служить мерой взаимодействия между атомом и фрагментом молекулы.

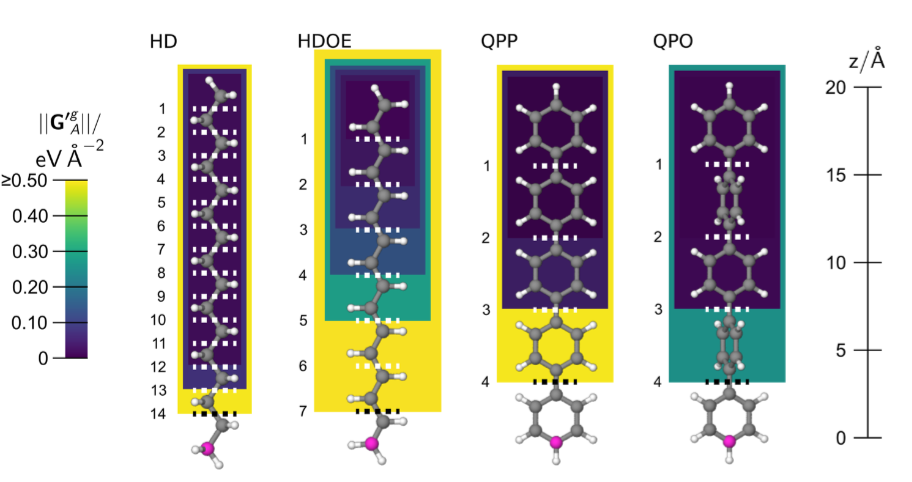
Применяя ||G_A^’g|| для анализа тестовых молекул, авторами были получены результаты, согласующиеся с применением величины ||h_AB||, характеризующей взаимодействие между атомами, но на этот раз стало доступно выделение фрагментов полной молекулы:

Предложенный метод был применен авторами к анализу взаимодействий в MOF-5, и был получен ряд интересных результатов, с которым мы предлагаем ознакомиться заинтересованным читателям: