20 NUMBER
https://search.aepiot.com/search.html?q=20%20NUMBERGo

Natural numberIn mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers 0, 1, 2, 3, ..., while others start with 1, defining them as the positive integers 1, 2, 3, ... . Some authors acknowledge both definitions whenever convenient. Sometimes, the whole numbers are the natural numbers as well as zero. In other cases, the whole numbers refer to all of the integers, including negative integers. The counting numbers are another term for the natural numbers, particularly in primary education, and are ambiguous as well although typically start at 1. The natural numbers are used for counting things, like "there are six coins on the table", in which case they are called cardinal numbers. They are also used to put things in order, like "this is the third largest city in the country", which are called ordinal numbers. Natural numbers are also used as labels, like jersey numbers on a sports team, where they serve as nominal numbers and do not have mathematical properties. The natural numbers form a set, commonly symbolized as a bold N or blackboard bold N {\displaystyle \mathbb {N} } . Many other number sets are built from the natural numbers. For example, the integers are made by adding 0 and negative numbers. The rational numbers add fractions, and the real numbers add all infinite decimals. Complex numbers add the square root of −1. This chain of extensions canonically embeds the natural numbers in the other number systems. Natural numbers are studied in different areas of math. Number theory looks at things like how numbers divide evenly (divisibility), or how prime numbers are spread out. Combinatorics studies counting and arranging numbered objects, such as partitions and enumerations.
In connection with: Natural number
Title combos: number Natural
Description combos: used numbers looks numbers The natural largest the in
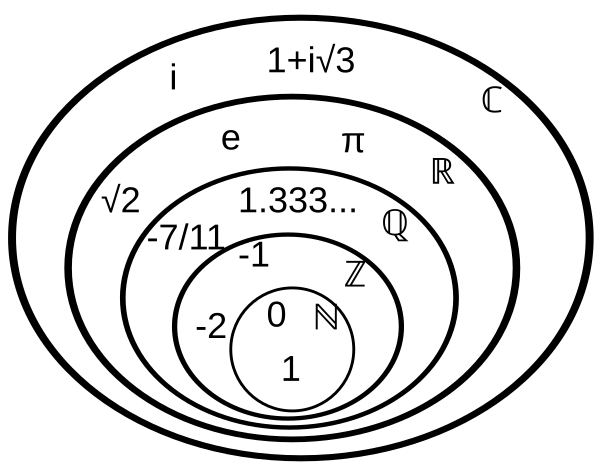
NumberA number is a mathematical object used to count, measure, and label. The most basic examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can be represented by symbols, called numerals; for example, "5" is a numeral that represents the number five. As only a relatively small number of symbols can be memorized, basic numerals are commonly organized in a numeral system, which is an organized way to represent any number. The most common numeral system is the Hindu–Arabic numeral system, which allows for the representation of any non-negative integer using a combination of ten fundamental numeric symbols, called digits. In addition to their use in counting and measuring, numerals are often used for labels (as with telephone numbers), for ordering (as with serial numbers), and for codes (as with ISBNs). In common usage, a numeral is not clearly distinguished from the number that it represents. In mathematics, the notion of number has been extended over the centuries to include zero (0), negative numbers, rational numbers such as one half ( 1 2 ) {\displaystyle \left({\tfrac {1}{2}}\right)} , real numbers such as the square root of 2 ( 2 ) {\displaystyle \left({\sqrt {2}}\right)} and π, and complex numbers which extend the real numbers with a square root of −1 (and its combinations with real numbers by adding or subtracting its multiples). Calculations with numbers are done with arithmetical operations, the most familiar being addition, subtraction, multiplication, division, and exponentiation. Their study or usage is called arithmetic, a term which may also refer to number theory, the study of the properties of numbers. Besides their practical uses, numbers have cultural significance throughout the world. For example, in Western society, the number 13 is often regarded as unlucky, and "a million" may signify "a lot" rather than an exact quantity. Though it is now regarded as pseudoscience, belief in a mystical significance of numbers, known as numerology, permeated ancient and medieval thought. Numerology heavily influenced the development of Greek mathematics, stimulating the investigation of many problems in number theory which are still of interest today. During the 19th century, mathematicians began to develop many different abstractions which share certain properties of numbers, and may be seen as extending the concept. Among the first were the hypercomplex numbers, which consist of various extensions or modifications of the complex number system. In modern mathematics, number systems are considered important special examples of more general algebraic structures such as rings and fields, and the application of the term "number" is a matter of convention, without fundamental significance.
In connection with: Number
Description combos: an or the numbers as is of numbers throughout
20 (number)20 (twenty) is the natural number following 19 and preceding 21. A group of twenty units is sometimes referred to as a score.
In connection with: 20 (number)
Title combos: 20 number
Description combos: group following twenty units twenty is is sometimes of
20Twenty or 20 may refer to: 20 (number), the natural number following 19 and preceding 21 one of the years 20 BC, AD 20, 1920, 2020
In connection with: 20
Description combos: or 2020 20 number and 20 and following 2020

English languageEnglish is a West Germanic language that developed in early medieval England and has since become a global lingua franca. The namesake of the language is the Angles, one of the Germanic peoples that migrated to Britain after its Roman occupiers left. English is the most spoken language in the world, primarily due to the global influences of the former British Empire (succeeded by the Commonwealth of Nations) and the United States. English is the third-most spoken native language, after Mandarin Chinese and Spanish; it is also the most widely learned second language in the world, with more second-language speakers than native speakers. English is either the official language or one of the official languages in 57 sovereign states and 30 dependent territories, making it the most geographically widespread language in the world. In the United Kingdom, the United States, Australia, and New Zealand, it is the dominant language for historical reasons without being explicitly defined by law. It is a co-official language of the United Nations, the European Union, and many other international and regional organisations. It has also become the de facto lingua franca of diplomacy, science, technology, international trade, logistics, tourism, aviation, entertainment, and the Internet. English accounts for at least 70% of total native speakers of the Germanic languages, and Ethnologue estimated that there were over 1.4 billion speakers worldwide as of 2021. Old English emerged from a group of West Germanic dialects spoken by the Anglo-Saxons. Late Old English borrowed some grammar and core vocabulary from Old Norse, a North Germanic language. Then, Middle English borrowed vocabulary extensively from French dialects, which are the source of approximately 28% of Modern English words, and from Latin, which is the source of an additional 28%. While Latin and the Romance languages are thus the source for a majority of its lexicon taken as a whole, English grammar and phonology retain a family resemblance with the Germanic languages, and most of its basic everyday vocabulary remains Germanic in origin. English exists on a dialect continuum with Scots; it is next-most closely related to Low Saxon and Frisian.
In connection with: English language
Title combos: English language
Description combos: Old phonology succeeded English peoples Australia with organisations New

Rational numberIn mathematics, a rational number is a number that can be expressed as the quotient or fraction p q {\displaystyle {\tfrac {p}{q}}} of two integers, a numerator p and a non-zero denominator q. For example, 3 7 {\displaystyle {\tfrac {3}{7}}} is a rational number, as is every integer (for example, − 5 = − 5 1 {\displaystyle -5={\tfrac {-5}{1}}} ). The set of all rational numbers is often referred to as "the rationals", and is closed under addition, subtraction, multiplication, and division by a nonzero rational number. It is a field under these operations and therefore also called the field of rationals or the field of rational numbers. It is usually denoted by boldface Q, or blackboard bold Q . {\displaystyle \mathbb {Q} .} A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: 3/4 = 0.75), or eventually begins to repeat the same finite sequence of digits over and over (example: 9/44 = 0.20454545...). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see Repeating decimal § Extension to other bases). A real number that is not rational is called irrational. Irrational numbers include the square root of 2 ( 2 {\displaystyle {\sqrt {2}}} ), π, e, and the golden ratio (φ). Since the set of rational numbers is countable, and the set of real numbers is uncountable, almost all real numbers are irrational. The field of rational numbers is the unique field that contains the integers, and is contained in any field containing the integers. In other words, the field of rational numbers is a prime field. A field has characteristic zero if and only if it contains the rational numbers as a subfield. Finite extensions of Q {\displaystyle \mathbb {Q} } are called algebraic number fields, and the algebraic closure of Q {\displaystyle \mathbb {Q} } is the field of algebraic numbers. In mathematical analysis, the rational numbers form a dense subset of the real numbers. The real numbers can be constructed from the rational numbers by completion, using Cauchy sequences, Dedekind cuts, or infinite decimals (see Construction of the real numbers).
In connection with: Rational number
Title combos: number Rational
Description combos: Dedekind every are displaystyle multiplication closure real displaystyle zero
20 Number Ones20 Number Ones is the first greatest hits album by American country singer Thomas Rhett. It was released through Valory on September 29, 2023. It is a compilation of his first 20 number-one country music singles, starting with "It Goes Like This" and presented in chronological order. A new track, "Mamaw's House", was also included and became his 21st overall number one at the Billboard Country Airplay chart in 2024. The number "20 Number Ones" includes songs that topped the Country Aircheck/MediaBase chart. It traces Rhett's path over the last 10 years.
In connection with: 20 Number Ones
Title combos: Number 20 Ones Number 20
Description combos: Ones on greatest hits Ones traces Ones number songs
Quick Access
Tag Explorer
Discover Fresh Ideas in the Universe of aéPiot
MultiSearch | Search | Tag Explorer
SHEET MUSIC | DIGITAL DOWNLOADS