110. Balanced Binary Tree

مسئله: تشخیص درخت ارتفاع-موازنه (Height-Balanced Tree)

فرض کنید یک درخت دودویی به شما داده شده است. بررسی کنید که آیا این درخت ارتفاع-موازنه (height-balanced) است یا خیر.

درخت ارتفاع-موازنه: درختی است که در آن بیشترین اختلاف ارتفاع بین هر زیر-درخت چپ و راست از یک گره، بیشتر از ۱ نباشد.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true

محدودیت‌ها:

• تعداد گره‌ها در درخت بین ۰ تا ۵۰۰۰ قرار دارد.
• مقدار گره‌ها بین ‎-۱۰۰۰۰ تا ۱۰۰۰۰ قرار دارد.

راه‌حل ۱: بازگشتی پایین به بالا (Bottom-Up Recursion)

تابعی به نام height(root) برای محاسبه ارتفاع یک درخت دودویی تعریف می‌کنیم که منطق آن به شرح زیر است:

• اگر درخت دودویی root تهی (null) باشد، مقدار ۰ را برگردانیم.
• در غیر این صورت، به طور بازگشتی ارتفاع‌های زیر درخت چپ و راست را که به ترتیب با l و r نشان داده می‌شوند، محاسبه کنیم. اگر هر کدام از l یا r برابر با ۱- (منفی یک) باشند، یا اختلاف مطلق بین l و r بیشتر از ۱ باشد، در این صورت ۱- (منفی یک) را برگردانیم. در غیر این صورت، max(l, r) + ۱ را برگردانیم (حداکثر ارتفاع بین زیر درخت چپ و راست به علاوه ۱).

بنابراین، اگر تابع height(root) مقدار ۱- (منفی یک) را برگرداند، به این معنی است که درخت دودویی root ارتفاع-موازنه نیست. در غیر این صورت، این درخت ارتفاع-موازنه است.

پیچیدگی زمانی این الگوریتم O(n) و پیچیدگی فضایی آن O(n) است. در اینجا، n تعداد گره‌ها در درخت دودویی می‌باشد.

/**
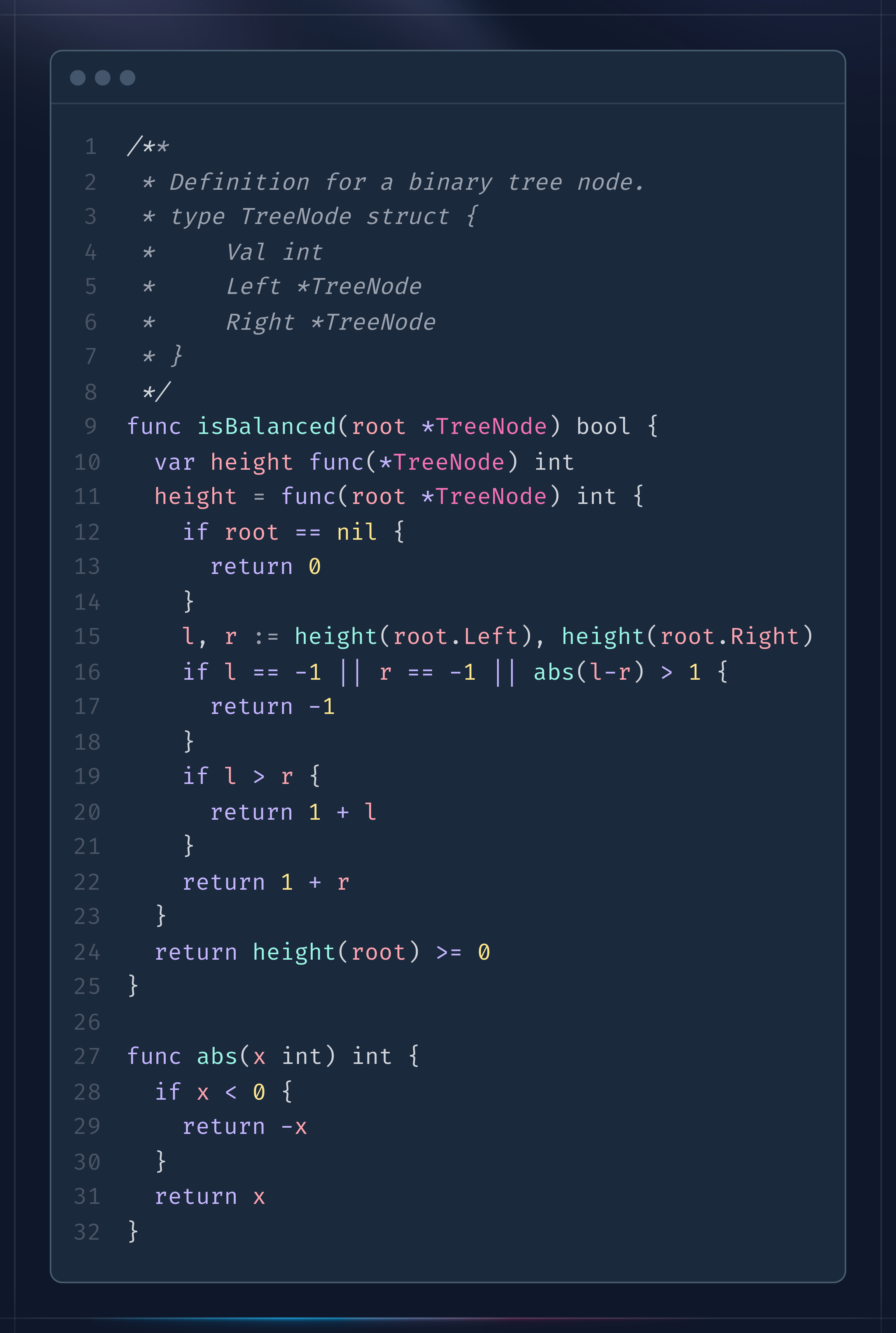
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isBalanced(root *TreeNode) bool {
 var height func(*TreeNode) int
 height = func(root *TreeNode) int {
  if root == nil {
   return 0
  }
  l, r := height(root.Left), height(root.Right)
  if l == -1 || r == -1 || abs(l-r) > 1 {
   return -1
  }
  if l > r {
   return 1 + l
  }
  return 1 + r
 }
 return height(root) >= 0
}

func abs(x int) int {
 if x < 0 {
  return -x
 }
 return x
}