Признаки равенства треугольников.

Треугольник — это геометрическая фигура, состоящая из трех точек,  

не лежащих на одной прямой, соединенных отрезками.  

 Первый признак равенства треугольников: треугольники равны, если у них равны две стороны и угол между ними. 

 Второй признак равенства треугольников: треугольники равны, если у них равны два угла и сторона между ними.  

Третий признак равенства треугольников: треугольники равны, если у них равны три стороны.  

Решение задач: 1.

1) AB=AD (по условию)

2) ∠BAC=∠DAC (по условию)

3) AC — общая сторона.

Следовательно, ∆ABC=∆ADC (по двум сторонам и углу между ними, то есть по первому признаку равенства треугольников).

Что и требовалось доказать.

2.

1) AO=BO (по условию)

2) CO=DO (по условию).

Для равенства треугольников осталось найти третью пару равных элементов. Это — углы AOC и BOD.

3) ∠AOC = ∠BOD (как вертикальные).

Все три пункта первого признака равенства треугольников есть. Следовательно, ∆AOC=∆BOD (по двум сторонам и углу между ними).

Что и требовалось доказать.

3.

Доказательство: Определяем, равенство каких элементов дано в условии. Записываем доказательство.

1) AB=AC (по условию)

2) AF=AK (по условию)

3) ∠A — общий.

Все три пункта первого признака равенства треугольников выполнены.

Следовательно, ∆ABK=∆ACF (по двум сторонам и углу между ними).

Что и следовало доказать.

4.

Доказательство:

Рассмотрим ∆AKM и ∆BMK.

1) MK — общая сторона.

2) ∠AMK=∠BKM (по условию).

Следовательно, ∆AKM=∆BMK (по стороне и двум прилежащим к ней углам, то есть, по второму признаку равенства треугольников).

Что и требовалось доказать.

5.

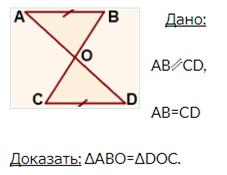
Доказательство:

1) AB=CD (по условию).

2) ∠ABO=∠DCO (как внутренние накрест лежащие при AB∥CD и секущей BC).

3) ∠BAO=∠CDO (как внутренние накрест лежащие при AB∥CD и секущей AD).

Следовательно, ∆ABO=∆DOC (по стороне и двум прилежащим к ней углам).

Что и требовалось доказать.

6.

Доказательство:

Рассмотрим треугольники AFC и BFD.

1) ∠AFC =∠BFD (по условию).

2) CF=DF (как боковые стороны равнобедренного треугольника CFD).

3) ∠ACF=∠BDF (как смежные с равными углами: ∠FCD=∠FDC как углы при основании равнобедренного треугольника CFD).

Следовательно, ∆AFC = ∆BFD (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: AF=BF. Значит, ∆AFB — равнобедренный с основанием AB (по определению равнобедренного треугольника).

Что и требовалось доказать.

 7.

Доказательство:

Рассмотрим треугольники AFB и BKA.

 1) AF=BK (по условию).

2) AK=BF (по условию).

3) AB — общая сторона.

Следовательно, ∆AFB=∆BKA по третьему признаку равенства треугольников (по трем сторонам). Что и требовалось доказать.

8.

Доказательство

Проведем отрезок BD.

Рассмотрим ∆ABD и ∆CDB.

1) AB=CD (по условию).

2) AD=BC (по условию).

3) BD — общая сторона.

Следовательно, ∆ABD = ∆CDB (по трем сторонам).

Из равенства треугольников следует равенство соответствующих углов. Значит, ∠A=∠C.

Что и требовалось доказать.