Фрактал

Фракта́л ([лат.] fractus — дроблёный, сломанный, разбитый) — [множество], обладающее свойством [самоподобия] (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). В математике под фракталами понимают множества точек в [евклидовом пространстве], имеющие дробную метрическую размерность (в смысле [Минковского] или [Хаусдорфа]), либо метрическую размерность, отличную от [топологической], поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Самоподобные фигуры, повторяющиеся конечное число раз, называются предфракталами.

Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференцируемых функций (например, [функция Больцано], [функция Вейерштрасса], [множество Кантора]). Термин «фрактал» введён [Бенуа Мандельбротом] в [1975 году] и получил широкую известность с выходом в [1977 году] его книги «[Фрактальная геометрия природы]». Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно [визуализировать] эти структуры.

Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных ниже свойств:

• Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если рассмотреть небольшой фрагмент регулярной фигуры в очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, то есть на всех шкалах можно увидеть одинаково сложную картину.
• Является самоподобным или приближённо самоподобным.
• Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.

Многие объекты в природе обладают свойствами фрактала, например: побережья, облака, кроны деревьев, снежинки, система кровообращения, [альвеолы].

Примеры

Самоподобные множества с необычными свойствами в математике

Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:

• множество Кантора — нигде не плотное несчётное совершенное множество. Модифицировав процедуру, можно также получить нигде не плотное множество положительной длины;
• треугольник Серпинского («скатерть») и ковёр Серпинского — аналоги множества Кантора на плоскости;
• губка Менгера — аналог множества Кантора в трёхмерном пространстве;
• примеры Вейерштрасса и Ван дер Вардена нигде не дифференцируемой непрерывной функции;
• кривая Коха — несамопересекающаяся непрерывная кривая бесконечной длины, не имеющая касательной ни в одной точке;
• кривая Пеано — непрерывная кривая, проходящая через все точки квадрата;
• траектория броуновской частицы также с вероятностью 1 нигде не дифференцируема. Её хаусдорфова размерность равна двум.

Рекурсивная процедура получения фрактальных кривых

Существует простая [рекурсивная] процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены первый, второй и четвёртый шаги этой процедуры для кривой Коха.

Примерами таких кривых служат:

• кривая Коха (снежинка Коха),
• кривая Леви,
• кривая Минковского,
• Кривая Гильберта
• Ломаная (кривая) дракона (Фрактал Хартера-Хейтуэя),
• кривая Пеано.
• Кривая Мякишева

С помощью похожей процедуры получается [дерево Пифагора].

Фракталы как неподвижные точки сжимающих отображений

Свойство самоподобия можно математически строго выразить следующим образом. Пусть [Формула] — [сжимающие отображения] плоскости. Рассмотрим следующее отображение на множестве всех [компактных] (замкнутых и ограниченных) подмножеств плоскости:
[Формула]

Можно показать, что отображение [Формула] является сжимающим отображением на множестве [компактов] с [метрикой Хаусдорфа]. Следовательно, по [теореме Банаха], это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.

Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения [Формула] — отображения подобия, а [Формула] — число звеньев генератора.

Для [треугольника Серпинского] [Формула] и отображения [Формула], [Формула], [Формула] — [гомотетии] с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении [Формула].

В случае, когда отображения [Формула] — преобразования подобия с коэффициентами [Формула], [размерность] [Формула] фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения [Формула]. Так, для [треугольника Серпинского] получаем [Формула].

По той же [теореме Банаха], начав с любого компактного множества и применяя к нему итерации отображения [Формула], мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.

Фракталы в комплексной динамике

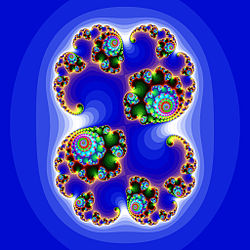
Фракталы естественным образом возникают при изучении нелинейных [динамических систем]. Наиболее изучен случай, когда динамическая система задаётся итерациями [многочлена] или [голоморфной функции комплексной переменной] на плоскости. Первые исследования в этой области относятся к началу 20 века и связаны с именами Фату и Жюлиа.

Пусть [Формула] — многочлен, [Формула] — [комплексное число]. Рассмотрим следующую последовательность: [Формула]

Нас интересует поведение этой последовательности при стремлении [Формула] к бесконечности. Эта последовательность может:

• стремиться к бесконечности,
• стремиться к конечному пределу,
• демонстрировать в пределе циклическое поведение, например:
• вести себя хаотично, то есть не демонстрировать ни один из трёх упомянутых типов поведения.

Множества значений [Формула], для которых последовательность демонстрирует один конкретный тип поведения, а также множества [точек бифуркации] между различными типами, часто обладают фрактальными свойствами.

Так, [множество Жюлиа] — множество точек бифуркации для многочлена [Формула] (или другой похожей функции), то есть тех значений [Формула], для которых поведение последовательности [Формула] может резко меняться при сколь угодно малых изменениях [Формула].

Другой вариант получения фрактальных множеств — введение параметра в многочлен [Формула] и рассмотрение множества тех значений параметра, при которых последовательность [Формула] демонстрирует определённое поведение при фиксированном [Формула]. Так, [множество Мандельброта] — это множество всех [Формула], при которых [Формула] для [Формула] и [Формула] не стремится к бесконечности.

Ещё один известный пример такого рода — [бассейны Ньютона].

Популярно создание красивых графических образов на основе комплексной динамики путём раскрашивания точек плоскости в зависимости от поведения соответствующих динамических систем. Например, для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления [Формула] к бесконечности (определяемой, скажем, как наименьший номер [Формула], при котором [Формула] превысит фиксированную большую величину [Формула]).

[Биоморфы] — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.

Стохастические фракталы

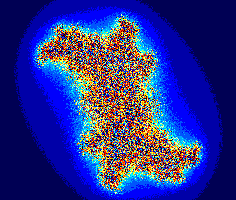
Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:

• траектория броуновского движения на плоскости и в пространстве;
• граница траектории броуновского движения на плоскости. В 2001 году Лоулер, Шрамм и Вернер доказали предположение Мандельброта о том, что её размерность равна 4/3.
• эволюции Шрамма-Лёвнера — конформно-инвариантные фрактальные кривые, возникающие в критических двумерных моделях статистической механики, например, в модели Изинга и перколяции.
• различные виды рандомизированных фракталов, то есть фракталов, полученных с помощью рекурсивной процедуры, в которую на каждом шаге введён случайный параметр. Плазма — пример использования такого фрактала в компьютерной графике.

Природные объекты, обладающие фрактальными свойствами

• В живой природе:
• В неживой природе:

Применение

Естественные науки

В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких как [турбулентное] течение жидкости, сложные процессы [диффузии]-[адсорбции], пламя, облака и тому подобное. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов). После создания кривой Коха было предложено использовать её при вычислении протяжённости береговой линии.

Радиотехника