Android
15.4.Simulación de caída con ligadura
Página 17 de 25
15. ANIMACIONES
En el capítulo anterior hemos introducido los conceptos necesarios para realizar animaciones, es decir, introducir sensación de movimiento en un texto o en general un gráfico, modificando rápidamente el dibujo de la pantalla. Es como ver una película, que consiste en una sucesión de imágenes o fotogramas.
Hasta ahora hemos mostrado contadores dinámicos que cambian con el tiempo. A continuación, animaremos otros objetos gráficos imprimiéndoles distintos tipos de movimiento.
15.1. Movimiento uniforme. La bola botadora
Comenzaremos con el movimiento más simple: una bola, representada por un círculo rojo, que inicialmente está en la parte superior de la pantalla y se mueve hacia abajo con velocidad constante. Cuando llegue al borde inferior invertiremos su velocidad, moviéndose hacia arriba. Al llegar arriba, volvemos a invertir su velocidad y el movimiento se repite. Para este programa no utilizaremos la interfaz de usuario de main.xml, sino que dibujaremos directamente sobre un canvas. El grueso del programa es la clase DinamicaView, que extiende a View e implementa la interfaz Runnable. El programa es el siguiente:
package es.ugr.amaro.movimientorectilineo;
import android.app.Activity;
public class MovimientoRectilineo extends Activity {
boolean continuar=true;
float velocidad=0.5f;
int dt=10;
int tiempo=0;
Thread hilo=null;
DinamicaView dinamica;
/** Called when the activity is first created. */
@Override
public void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
dinamica=new DinamicaView(this);
setContentView(dinamica);
hilo = new Thread(dinamica);
hilo.start();
}
// detenemos el hilo si pausa
@Override
public void onPause(){
super.onPause();
continuar=false;
}
// reiniciamos el hilo si resume
@Override
public void onResume(){
super.onResume();
continuar=true;
if(hilo==null){
hilo=new Thread(dinamica);
hilo.start();
}
}
class DinamicaView extends View implements Runnable{
int x,y,ymax; // coordenadas
Paint paintFondo,paintParticula,paint;
public DinamicaView(Context context) {
super(context);
// Colores para el dibujo y tmaño del texto
paintFondo=new Paint();
paintParticula=new Paint();
paint=new Paint();
paintFondo.setColor(Color.WHITE);
paintParticula.setColor(Color.RED);
paint.setColor(Color.BLACK);
paint.setTextSize(30);
}
@Override
public void run() {
while(continuar){
tiempo=tiempo+dt;
// movimiento uniforme y=y+v*t
y=y+(int)(velocidad*dt);
// si llega abajo invertimos velocidad
if(y>ymax) velocidad=-velocidad;
// si llega arriba invertimos velocidad
if(y<0) velocidad=-velocidad;
postInvalidate();
try { Thread.sleep( dt ); }
catch ( InterruptedException e ){ ; } }
}
// obtiene geometria del canvas
@Override
protected void onSizeChanged(
int w, int h, int oldw,int oldh){
x=w/2;
y=0;
ymax=h;
}
@Override
public void onDraw(Canvas canvas ){
canvas.drawPaint(paintFondo);
canvas.drawCircle(x, y, 30, paintParticula);
canvas.drawText("y="+y, 50, 50, paint);
canvas.drawText("t="+tiempo, 50, 90, paint);
}
} // fin dinamica
}
Podemos ver dos capturas de pantalla en la figura 15.1. En el método onStart()instanciamos nuestro objeto View e iniciamos el hilo para la animación. En esta actividad implementamos también los métodos onPause() para detener el hilo en caso de abandonar la actividad y onResume() para reiniciar la actividad si volvemos a ella. Estos métodos deberían incluirse siempre, aunque por brevedad no los mostramos explícitamente en todos nuestros ejemplos.
Los parámetros que requiere el programa son la velocidad de la bola y el incremento de tiempo o retraso con el que redibujamos la pantalla:
float velocidad=0.5f;
int dt=10;

Figura 15.1. La pelota botadora.
Animamos al lector a modificar estos valores y ver lo que ocurre, teniendo en cuenta que el tiempo está expresado en unidades de milisegundos (ms) y la velocidad en pixeles/milisegundo (p/ms). Si la velocidad es demasiado grande, pongamos mayor de 10 p/ms, la bola recorrerá 10 pixeles en un milisegundo, una distancia demasiado grande para apreciar un cambio brusco de posición entre una pantalla y la siguiente. Si el tiempo dt es demasiado grande, pongamos mayor que 50ms (equivalente a 20 fotogramas por segundo), apreciaremos el tiempo que la pantalla está parada y el movimiento nos parecerá parpadeante. Los valores más adecuados para que el movimiento nos parezca suave y fluido son velocidad < 1 y dt < 10.
En esta aplicación hemos definido el método onSizeChanged para extraer los nuevos valores de anchura y altura del canvas en el caso de que la geometría de éste se modifique, principalmente al girar el teléfono (giro que en el emulador realizamos pulsando Ctrl-F11).
La posición de la bola se calcula en el método run(), donde su coordenada y se incrementa según la ecuación del movimiento:

Teniendo en cuenta que la velocidad es de tipo float y las coordenadas y tiempo son enteros, esta ecuación se implementa en nuestro programa como:
y = y + (int) (velocidad*dt);
Inicialmente la velocidad es positiva y la pelota cae hacia abajo. Cuando la pelota llega a la base de la pantalla invertimos su velocidad (la hacemos negativa):
if(y > ymax) velocidad=-velocidad;
y el sentido de su movimiento se invierte, dirigiéndose hacia arriba. Al llegar arriba invertimos de nuevo su velocidad:
if(y <0 ) velocidad= -velocidad;
y el movimiento se repite estacionariamente.
15.2. Movimiento acelerado. La bola botadora II
Para simular otros elementos de la dinámica introduzcamos una aceleración, que represente la fuerza de la gravedad:
float velocidad=0.05f;
float aceleracion=0.01f;
int dt=1;
Modifiquemos el método run() trasladando todo el cálculo de la posición a un nuevo método cambiaPosición(). Esto nos permitirá modificar fácilmente el programa si queremos añadir otro tipo de trayectorias más adelante. Bastará con modificar este último método.
@Override
public void run() {
while(continuar){
cambiaPosicion();
postInvalidate();
try { Thread.sleep( dt ); }
catch ( InterruptedException e ){ ; }
}
}
public void cambiaPosicion() {
tiempo=tiempo+dt;
// movimiento y=y+v*dt
y=y+(int)(velocidad*dt);
// fuerza v=v+a*dt
velocidad=velocidad+aceleracion*dt;
// si llega abajo invertimos velocidad
if(y>ymax) velocidad=-Math.abs(velocidad);
// si llega arriba invertimos velocidad
if(y<0) velocidad=Math.abs(velocidad);
}
La única modificación que hemos hecho es introducir el cambio de velocidad en cada intervalo de tiempo según la ecuación:

ya que la aceleración representa precisamente el cambio infinitesimal de la velocidad:
velocidad = velocidad + aceleración * dt;
Esta aceleración puede también interpretarse aquí como producida por una fuerza sobre una partícula de masa igual a uno m=1, ya que, según la ecuación de Newton, F=ma. Nótese que en CambiaPosicion() hemos cambiado las líneas para invertir la velocidad en los extremos, introduciendo explícitamente su signo (es decir, más o menos su valor absoluto). Esto es debido a que, por problemas de redondeo, podría darse el caso de que la partícula sobrepase el borde y la inversión de velocidad no sea suficiente para sacarla, en cuyo caso quedará indefinidamente fuera de la pantalla y su velocidad continuará invirtiéndose en cada iteración.
En la figura 15.2 vemos dos capturas de pantalla. Aunque en estas imágenes estáticas no es posible apreciar el movimiento de la simulación, hemos escrito en la pantalla también el valor de la velocidad, para demostrar cómo está cambiando continuamente. También hemos desplazado la posición x de la bola para dejar sitio al texto. Este es el nuevo método onDraw():
@Override
public void onDraw(Canvas canvas ){
canvas.drawPaint(paintFondo);
canvas.drawCircle(x+100, y, 30, paintParticula);
canvas.drawText("y="+y, 50, 50, paint);
canvas.drawText("t="+tiempo, 50, 90, paint);
canvas.drawText("v="+velocidad, 50, 130, paint);
}

Figura 15.2. La bola botadora acelerada. En la figura de la derecha la velocidad es tan grande que la captura de la pantalla no ha captado la imagen de la bola, en el momento en que cambiaba de posición.
15.3. Conservación de la energía
Si observamos detenidamente la simulación anterior durante unos minutos en el emulador o en el teléfono, veremos que la velocidad va aumentando poco a poco y puede llegar a hacerse el doble en unos minutos. En particular, su energía no se conserva. Esto es consecuencia de la poca precisión en la resolución de la ecuación del movimiento, que hemos implementado de forma incremental, con un paso de tiempo de 1 ms, lo que hace que la solución sea inestable para tiempos muy largos. Aunque la ecuación puede resolverse con más precisión usando métodos matemáticos conocidos, en este caso vamos a aplicar el principio de conservación de la energía, que es una condición que debe verificar nuestra trayectoria y que mejorará su estabilidad. Como es sabido del curso de física elemental, la energía asociada a una fuerza constante en el eje y es la suma de energía cinética y energía potencial:

donde el signo menos en la energía potencial se debe a que en el dispositivo el eje y apunta hacia abajo. De esta fórmula podemos despejar el valor de y:
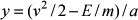
Esta es la fórmula que emplearemos para calcular y. En principio tendríamos que conocer la masa de la partícula m, pero veamos que en este problema es irrelevante. La energía debe mantenerse constante e igual a la energía inicial, para y=0, que es:

Sustituyendo en la ecuación anterior, encontramos que la coordenada y viene dada por:

que no depende de la masa. Esto quiere decir que podemos elegir cualquier valor de la masa, por ejemplo m=1. Si calculamos la coordenada y mediante esta fórmula, la energía de nuestra bola se conservará, lo que contribuye a la estabilidad y periodicidad de su movimiento.
Para implementar la conservación de la energía basta modificar el método cambiaPosición() de la siguiente forma:
public void cambiaPosicion() {
tiempo=tiempo+dt;
// fuerza v=v+a*dt
velocidad=velocidad+aceleracion*dt;
// conservacion de la energia
float cinetica=velocidad*velocidad/2;
y=(int)((cinetica-energia)/aceleracion);
// si llega abajo invertimos velocidad
if(y>ymax) velocidad=-Math.abs(velocidad);
// si llega arriba invertimos velocidad
if(y<0) velocidad=Math.abs(velocidad);
}
Previamente hay que declarar la variable de clase energia en la clase principal:
float energia;
y hay que definir el valor constante de ésta igual a la energía inicial en el método onSizeChanged():
@Override
protected void onSizeChanged(
int w, int h, int oldw,int oldh){
x=w/2;
y=0;
ymax=h;
energia=0.5f * velocidad * velocidad - aceleracion * y;
}
Con estos cambios el movimiento se mantiene estable, puesto que forzamos que la energía sea constante y, con ello, también la velocidad máxima de la bola.
15.4. Simulación de caída con ligadura
Una ligadura mecánica es una restricción sobre el movimiento de un cuerpo. En la siguiente actividad simularemos el movimiento de un cuerpo, representado por un círculo rojo, que cae por la gravedad siguiendo una trayectoria parabólica, por ejemplo una bola que se deja caer en un pozo con dicha forma. La figura 15.3 muestra dos instantáneas del programa Android durante su caída. Inicialmente está localizado en las coordenadas (xmin,ymin)=(0,0). La ecuación de la parábola que está dibujada es:

donde y
max
es la altura del canvas y x
0
es la mitad de su anchura. En la actividad hemos introducido una clase Trayectoria con métodos para calcular las propiedades de la trayectoria. Por ejemplo getY( x ) proporciona el valor de y en función de x.
Esta simulación está basada en el ejemplo de la pelota botadora de la sección anterior. La fuerza que se ejerce sobre la partícula está dirigida en la dirección y (hacia abajo, pero y es positivo en nuestro sistema de coordenadas):

donde m=1 es la masa y a es la aceleración de la gravedad. Utilizaremos el principio de conservación de la energía:

donde T es la energía cinética, mv
2
/ 2 , y - may la energía potencial. A partir de esta ecuación podemos calcular la altura si conocemos la velocidad, como en el caso de la pelota botadora:


Figura 15.3. La partícula que cae con una ligadura y está obligada a seguir una parábola.
Finalmente, conocida la altura y, podemos conocer la coordenada horizontal a partir de la ecuación de la parábola inversa:

El problema es elegir enre las dos soluciones correspondientes a las dos posiciones posibles (izquierda o derecha). Nosotros lo haremos introduciendo una variable booleana, cambio, que cambia de valor cada vez que la partícula llega abajo y pasa por el punto inferior de la curva. Si la variable es true, se mueve hacia la izquierda y tomamos el signo menos. Si es false, se mueve hacia la derecha y tomamos el signo positivo.
Todo se reduce a calcular la velocidad en cada instante. El vector velocidad es siempre tangente a la curva de la trayectoria. Por tanto, conocemos su dirección y resta por calcular su magnitud o módulo v = | v |. En este caso, la trayectoria es una parábola f(x). El vector tangente a la gráfica de una función f(x) está determinado por su derivada:

Por otra parte, la componente tangencial de la aceleración es (ver Alonso-Finn, Eq. (5.43)):

Esta aceleración debe ser igual a la fuerza tangencial (para m=1), que es la componente de la fuerza gravitatoria en la dirección de la tangente T:

Por tanto, lo que hacemos es calcular el cambio en la velocidad en cada intervalo dt mediante:

El siguiente listado es el programa Java completo. La dinámica anterior está implementada en el método cambiaPosicion3(). Las propiedades de la trayectoria se calculan usando un objeto de la clase Trayectoria.
package es.ugr.ligaduras;
import android.app.Activity;
import android.content.Context;
import android.graphics.Canvas;
import android.graphics.Color;
import android.graphics.Paint;
import android.graphics.Paint.Style;
import android.graphics.Path;
import android.os.Bundle;
import android.view.View;
import android.view.View.OnClickListener;
public class Ligaduras extends Activity implements
OnClickListener{
boolean continuar=true;
float velocidad=0.1f;
float aceleracion=0.001f;
float energia;
int dt=1;
int tiempo=0;
Thread hilo=null;
DinamicaView dinamica;
Trayectoria trayectoria=new Trayectoria(100,100);
/** Called when the activity is first created. */
@Override
public void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
dinamica=new DinamicaView(this);
setContentView(dinamica);
dinamica.setOnClickListener(this);
;hilo = new Thread(dinamica);
hilo.start();
}
// detenemos el hilo si pausa
@Override
public void onPause(){
super.onPause();
continuar=false;
}
// reiniciamos el hilo si resume
@Override
public void onResume(){
super.onResume();
continuar=true;
if(hilo==null){
hilo=new Thread(dinamica);
hilo.start();
}
}
@Override
public void onClick(View v) {
// TODO Auto-generated method stub
continuar=!continuar;
if(continuar| hilo==null){
hilo=new Thread(dinamica);
hilo.start();
}
}
class DinamicaView extends View implements Runnable{
int x,y,xmin,ymin,ymax; // coordenadas
float tangenteX,tangenteY;
float tx,ty;
Paint paintFondo,paintParticula,paint,
paintCurva,paintVector;
Path path;
String control;
boolean cambio=true;
public DinamicaView(Context context) {
super(context);
// Colores para el dibujo y tamaño del texto
paintFondo=new Paint();
paintParticula=new Paint();
paint=new Paint();
paintFondo.setColor(Color.WHITE);
paintParticula.setColor(Color.RED);
paint.setColor(Color.BLACK);
paint.setTextSize(18);
paintCurva=new Paint();
paintCurva.setStyle(Style.STROKE);
paintVector=new Paint();
paintVector.setStrokeWidth(8);
paintVector.setColor(Color.BLACK);
}
// obtiene geometria del canvas
@Override
protected void onSizeChanged(
int w, int h, int oldw,int oldh){
x=w/2;
xmin=0;
y=0;
ymax=h-xmin;
float anchura=w;
float altura=h;
trayectoria=new Trayectoria(anchura,altura);
ymin=(int) trayectoria.getY(xmin);
energia=0.5f * velocidad * velocidad
- aceleracion * ymin;
control="anchura:"+anchura+" altura:"+altura;
// construye el path de la trayectoria
path=new Path();
path.moveTo(xmin,ymin);
for (int i=xmin; i<anchura-xmin;i++){
float xi=i;
float yi=trayectoria.getY(xi);
path.lineTo(xi,yi);
}
}
@Override
public void run() {
while(continuar){
cambiaPosicion3();
postInvalidate();
try { Thread.sleep( dt ); }
catch ( InterruptedException e ){ ; }
}
}
public void cambiaPosicion3() {
float[] tangente={0,0};
tiempo=tiempo+dt;
tangente=trayectoria.getTangente(x);
float tangenteX=tangente[0];
float tangenteY=tangente[1];
tx=tangenteX*velocidad;
ty=tangenteY*velocidad;
float aT=aceleracion*tangenteY;
velocidad=velocidad+aT*dt;
float cinetica=velocidad*velocidad/2;
float yfloat=((cinetica-energia)/aceleracion);
y=(int) yfloat;
if(y>=ymax) {
x=(int) (x+Math.signum(velocidad)*dt);
y=(int) trayectoria.getY(x);
cambio=!cambio;
}
if (cambio) x=(int) trayectoria.getX2(y);
else x=(int) trayectoria.getX1(y);
// si llega arriba invertimos velocidad
if(y<ymin)velocidad=-velocidad;
}
@Override
public void onDraw(Canvas canvas ){
canvas.drawPaint(paintFondo);
canvas.drawCircle(x, y, 30, paintParticula);
canvas.drawText("x="+x+" y="+y, 50, 50, paint);
canvas.drawText("t="+tiempo, 50, 90, paint);
canvas.drawText("v="+velocidad, 50, 130, paint);
canvas.restore();
canvas.drawPath(path,paintCurva);
canvas.drawText("Componentes de la
velocidad",50,170,paint);
float e=100; // escala para vector
canvas.drawLine(x,y, x+e*tx,y+e*ty,paintVector);
canvas.drawText("V",x+e*tx+20,y+e*ty-20,paint);
canvas.drawText("VX="+tx, 50,200, paint);
canvas.drawText("VY="+ty, 50,230, paint);
}
} // fin dinamica
// clase parara la trayectoria de una particula
class Trayectoria{
float yMax,x0;
Trayectoria(float anchura, float altura){
yMax=altura;
x0=anchura/2;
}
float getY(float x){
float xx0=(x-x0)/x0;
float y=yMax*(1-xx0*xx0);
return y;
}
// raiz positiva de la funcion inversa
float getX1(float y){
double raiz,radicando;
radicando=Math.max(0f,1-y/yMax);
raiz=Math.sqrt(radicando);
float x1=(float) (x0+x0*raiz);
return x1;
}
// raiz negativa de la funcion inversa
float getX2(float y){
double raiz,radicando;
radicando=Math.max(0f,1-y/yMax);
raiz=Math.sqrt(radicando);
float x2=(float) (x0-x0*raiz);
return x2;
}
// componente y del vector unitario tangente a la curva
float[] getTangente(float x){
float[] tangente=new float[2];
float xx0=(x-x0)/x0;
float derivada=-yMax*2*xx0/x0;
double denominador=Math.sqrt(1+derivada*derivada);
tangente[0]=(float) (1/denominador);
tangente[1]=(float) (derivada/denominador);
return tangente;
}
}
}
El resultado se ve en las figuras 15.3, 15.4 y 15.5. La posición y velocidad de la partícula se calculan en el método cambiaPosicion3(). Cuando la partícula llega arriba invertimos la velocidad para que vuelva a bajar en sentido opuesto. Existe un problema cuando la partícula llega abajo, al punto mínimo (figura 15.5), ya que la componente tangencial de la fuerza es cero, por lo que su velocidad no cambiaría y, por tanto, tampoco su altura. Si no hacemos nada más, la partícula llega al mínimo y se detiene. Pero la partícula debe seguir adelante puesto que su velocidad no es cero. Para que sea así, en este punto, debemos modificar la coordenada x de la partícula mediante:

y así conseguimos que la partícula siga adelante. Hay que tener cuidado, además, al calcular las coordenadas en pixeles, puesto que son números enteros y, por redondeo, es posible que dx=0.

Figura 15.4. La partícula que cae con una ligadura parabólica, en su trayectoria ascendente.

Figura 15.5. La partícula que cae cerca del mínimo del potencial