Решение задачи 72

Рассмотрим произвольный пятиугольник с равными сторонами, который не является правильным.

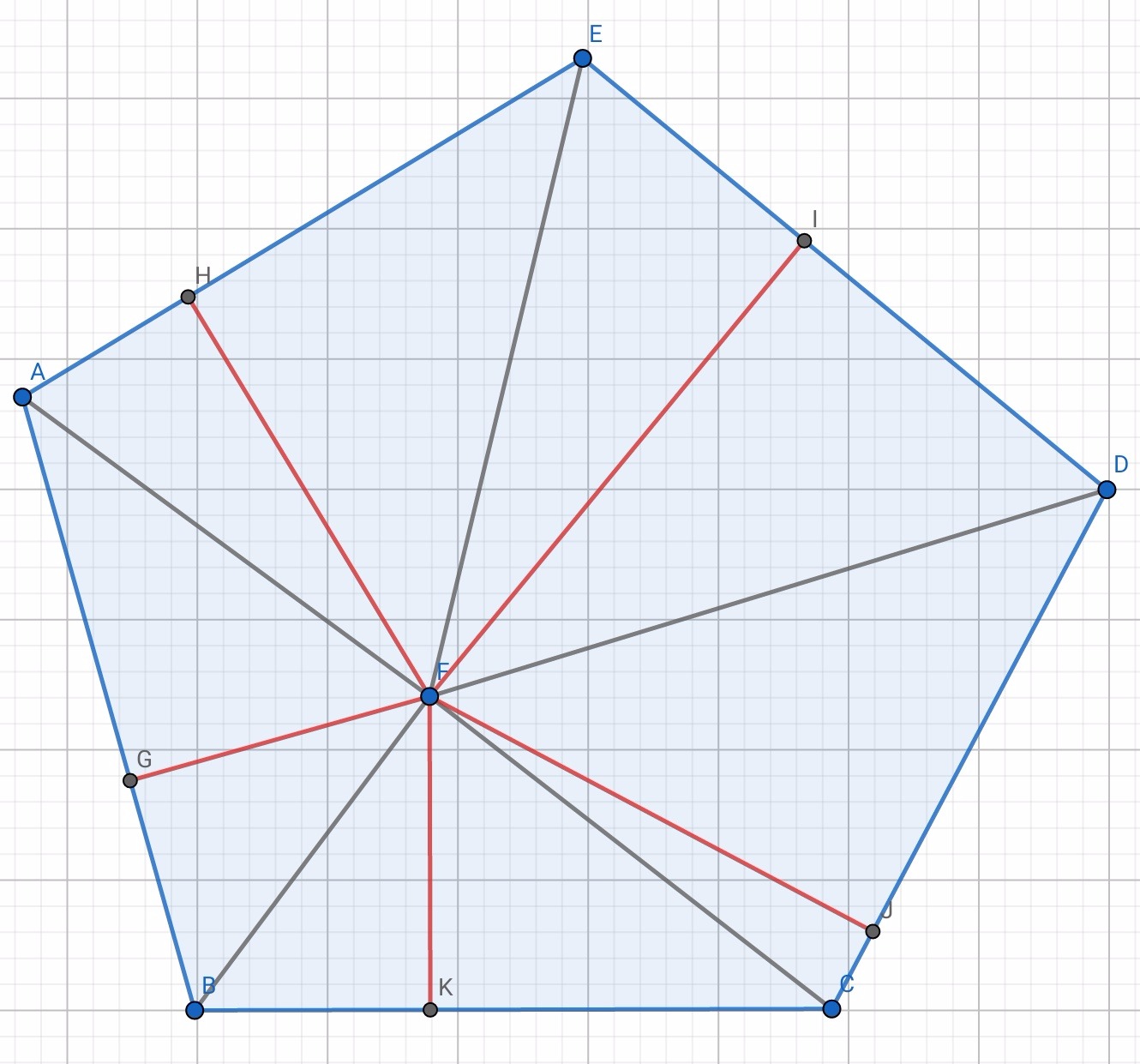
Давайте обозначим стороны пятиугольника как a1,a2,a3,a4,a5. Расстояния от произвольной точки F внутри пятиугольника до прямых, содержащих стороны: h1,h2,h3,h4,h5. Проведем отрезки соединяющие точку внутри пятиугольника с вершинами и рассмотрим суммарную площадь получившийся пяти треугольников : S = S1 +S2 + S3 + S4 + S5. Очевидно, что S равна площади всего пятиугольника и не зависит от выбора точки. С другой стороны, S = 0.5*a1*h1 + 0.5*a2*h2 + 0.5*a3*h3 + 0.5*a4*h4 + 0.5*a5*h5 = 0.5*a*(h1 + h2 + h3 + h4 + h5). В последнем равенстве мы использовали тот факт, что все стороны пятиугольника равны. Получаем:

h1 + h2 + h3 + h4 + h5 = 2S/a = const.

Таким образом мы показали, что в любом пятиугольнике с равными сторонами сумма расстояний от внутренней точки до прямых, содержащих стороны, не зависит выбора этой внутренней точки. При этом пятиугольник не обязан быть правильным.