Решение задачи 65

Поскольку координаты вершин четырехугольника - целые числа, то его вершины находится в узлах квадратной сетки. Давайте впишем четырехугольник в прямоугольник. Вот 2 примера такого прямоугольника:

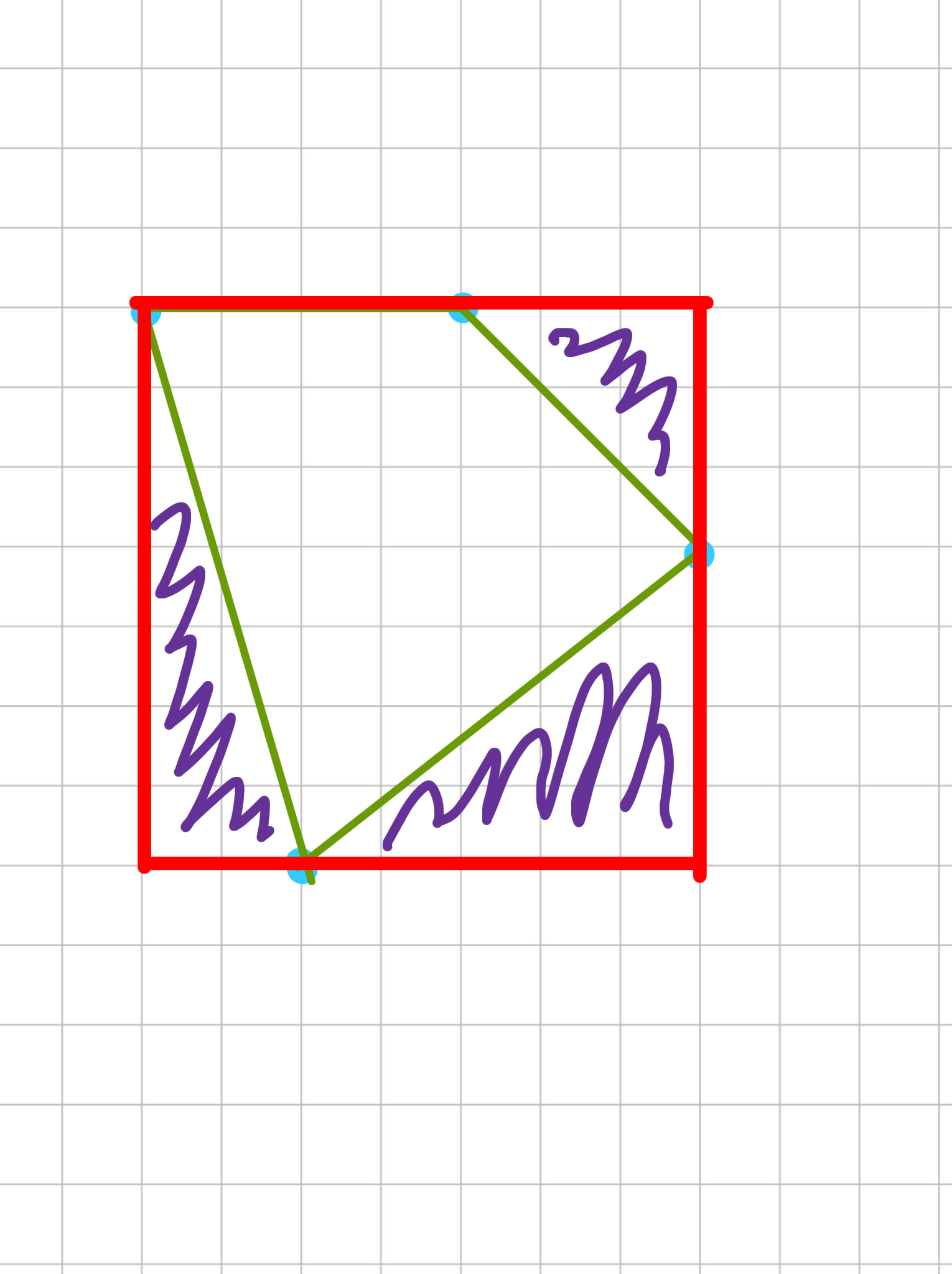
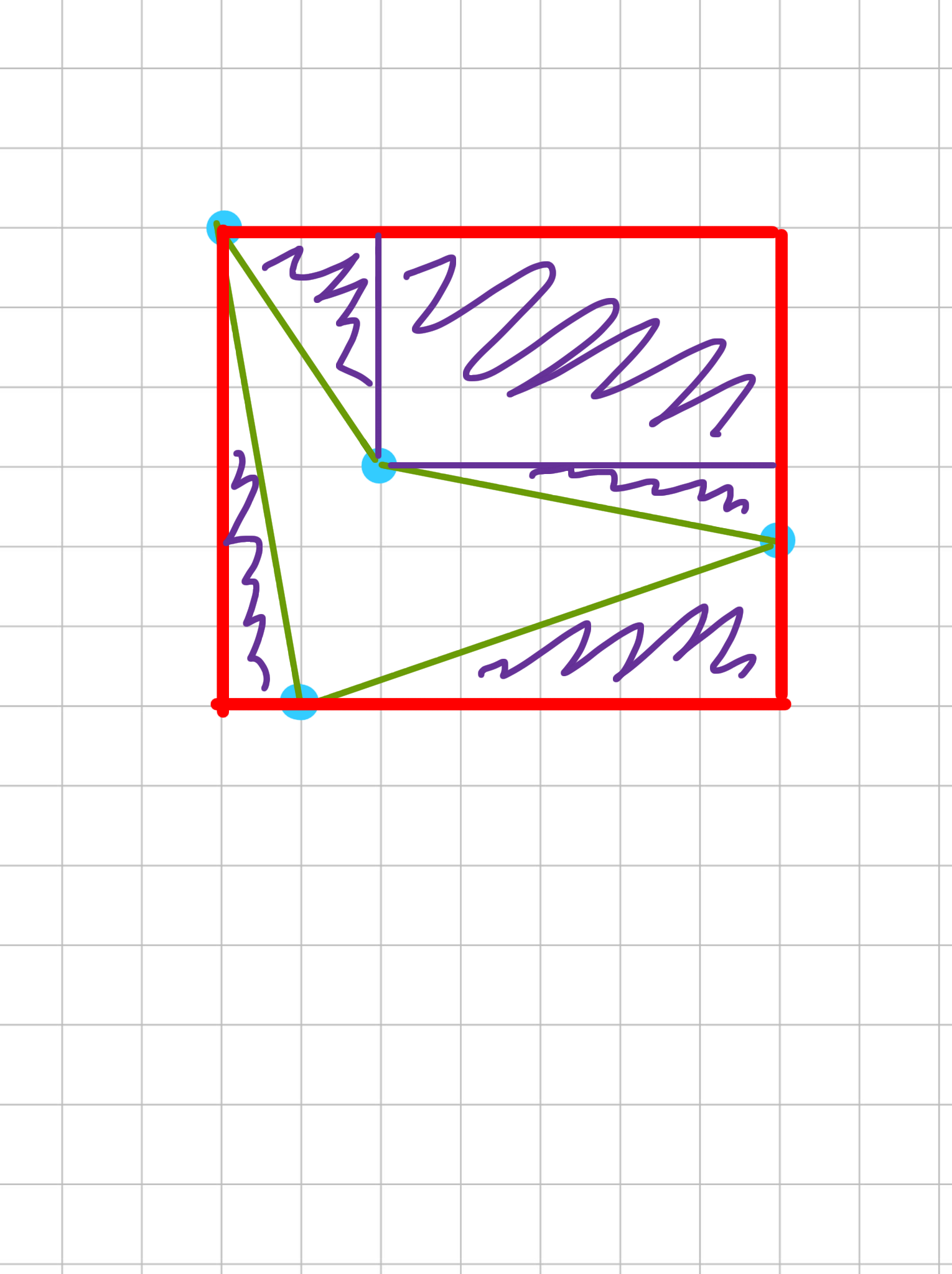
Четырехугольник вырезает из описанного прямоугольника какую-то часть. Понятно, что оставшуюся невырезанную часть прямоугольника можно разбить на прямоугольники и прямоугольные треугольники с вершинами в узлах сетки.

Давайте теперь предположим, что площадь исходного четырехугольника равняется 148,8. Площадь каждого прямоугольника с вершинами в узлах сетки (и со сторонами, параллельными сетке) - целое число. Площать каждого прямоугольника с вершинами в узлах сетки (и с катетами, параллельными сетке) - половина площади прямоугольника с вершинами в узлах сетки, значит площадь такого треугольника либо целое число, либо число, заканчивающееся на ......,5. Но сумма чисел, десятичная часть которых заканчивается на 0,5,8 (ровно одна восьмерка обязательно есть) не может быть целым числом (площадь описанного прямоугольника, очевидно, является целым числом).

Значит такого четырехугольника не бывает.