Решение задачи 247

Условие:

Между городами страны организованы двусторонние беспосадочные авиарейсы таким образом, что от каждого города до каждого другого можно добраться (возможно, с пересадками). Более того, для каждого города А, существует город B такой, что любой из остальных городов напрямую соединён либо с А, либо с B. Докажите, что можно от любого города добраться до любого другого не более, чем с двумя пересадками.

Решение:

Будем доказывать от противного. Предположим, что существуют какие-то два города X и Y, что кратчайший путь от X до Y проходит через города Z1,Z₂,...,Zn (n>2). На рисунке этот маршрут обозначен зелёным цветом.

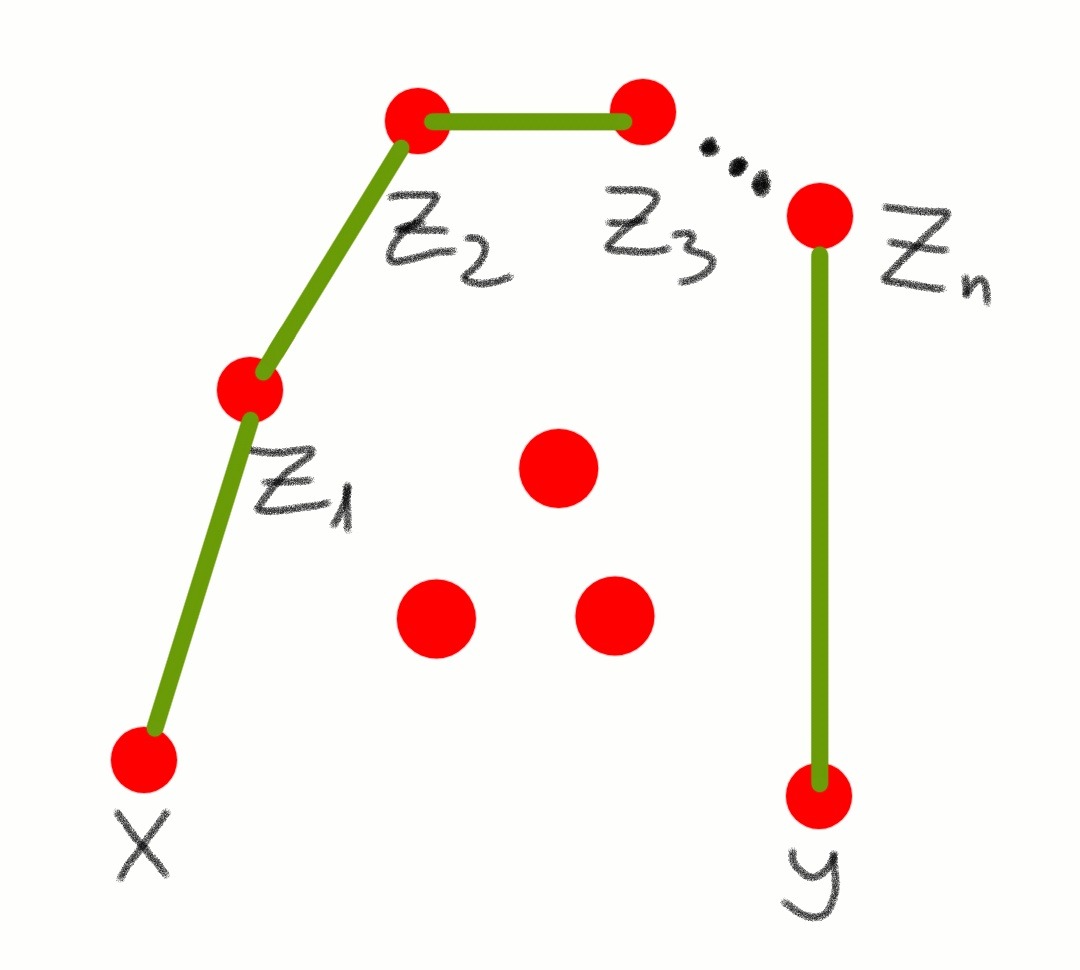
Замечание 1. Город X не может быть напрямую соединён с городом Z₂, т.к. иначе получился бы путь из X в Y, проходящий через города Z₂,...,Zn. То есть получился бы путь короче минимального, чего конечно же не может быть.

Замечание 2. Город Y не может быть напрямую соединён с городом Z₂ по абсолютно аналогичной причине.

Из условия задачи нам известно, что для города Z₂ существует город B такой, что любой другой город напрямую соединён либо с Z₂, либо с B.

Возможны три варианта: город B отличен от городов X и Y, город B совпадает с городом X, город B совпадает с городом Y.

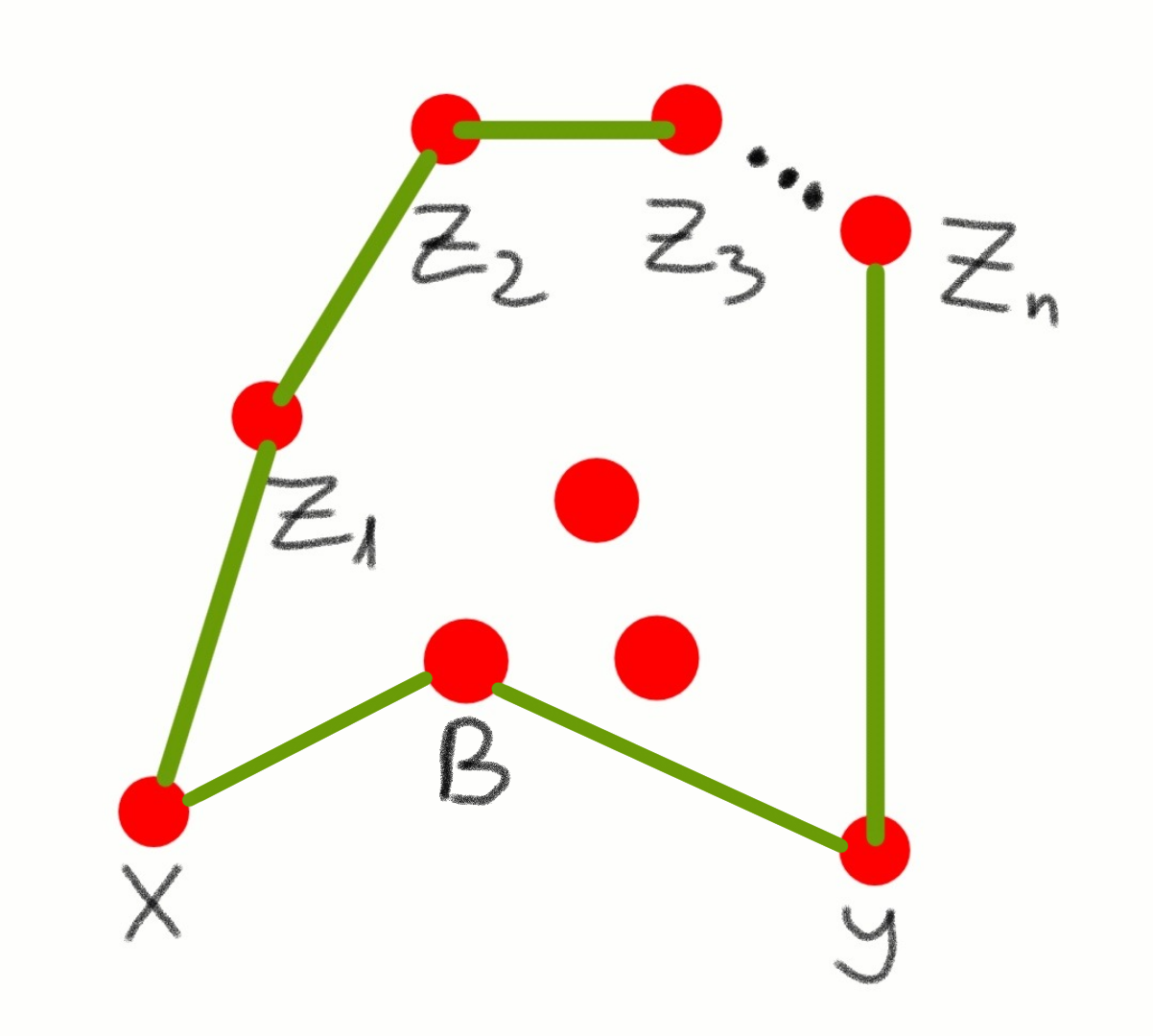
Рассмотрим первый случай. Согласно замечаниям 1 и 2, города X и Y не могут быть напрямую соединены с городом Z₂. Значит города X и Y должны быть напрямую соединены с городом B. Но в этом случае существует путь из X в Y всего с одной пересадкой через город B. Противоречие.

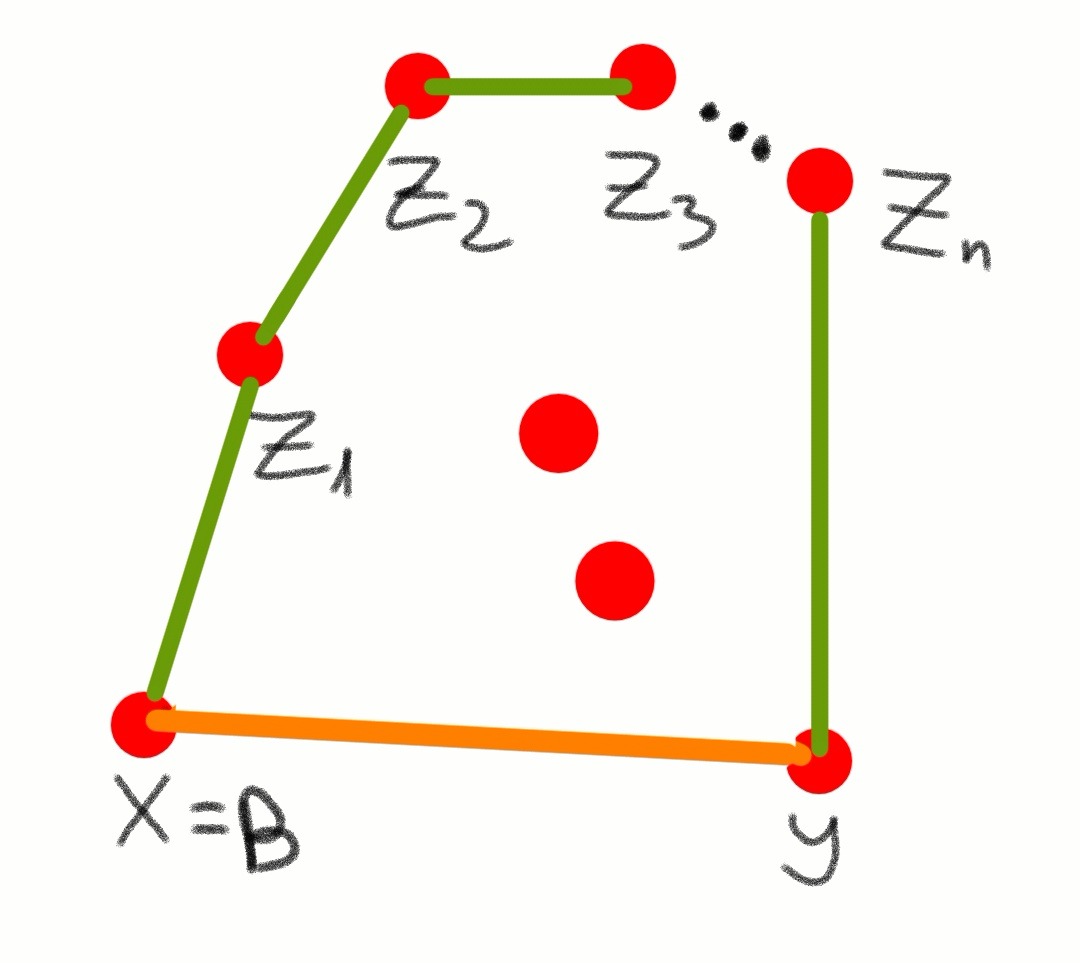
Во втором случае, согласно замечанию 2, город Y не может быть напрямую соединён с Z₂, поэтому он должен быть напрямую соединён с городом B, то есть с Х. Значит существует прямой маршрут из Х в Y. Противоречие.

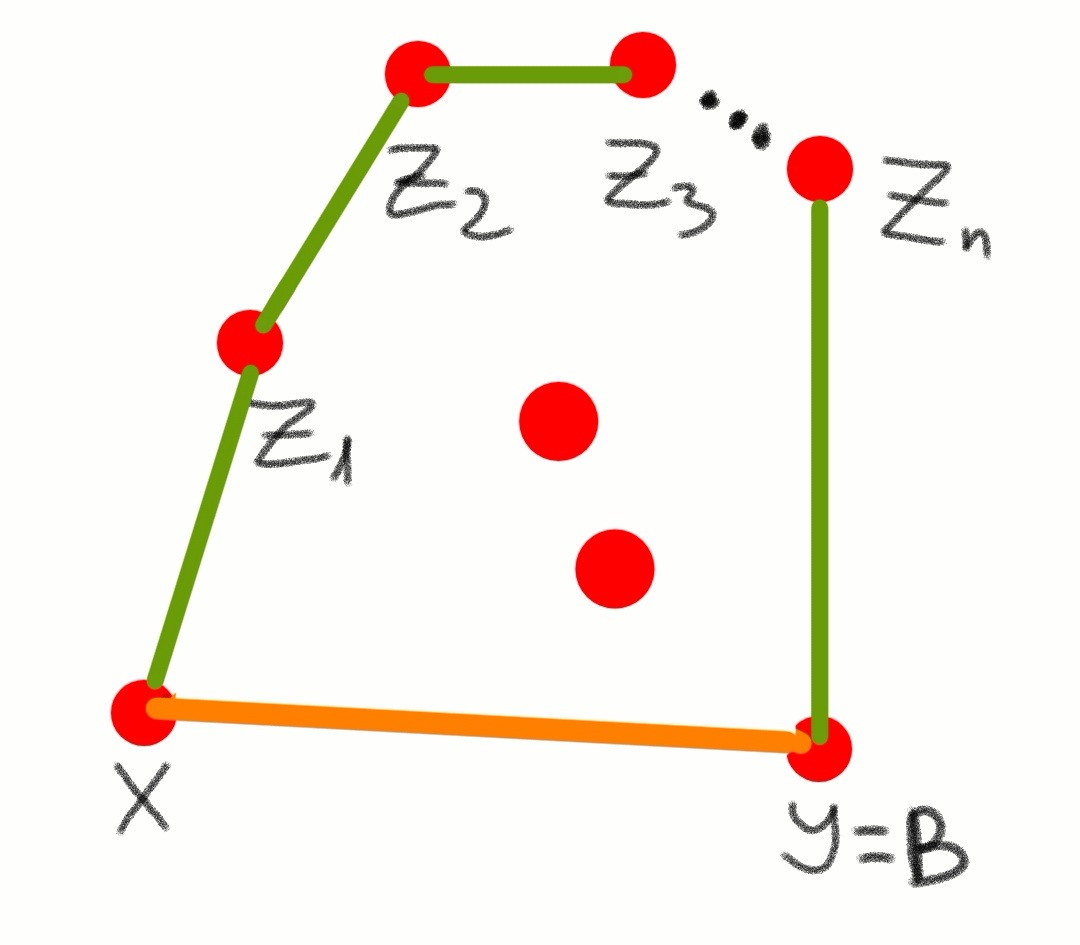
Аналогично и в третьем случае, согласно замечанию 1, город X не может быть напрямую соединён с Z₂, поэтому он должен быть напрямую соединён с городом B, то есть с Y. Значит существует прямой маршрут из Х в Y. Противоречие.

Как мы видим, в любом из возможных случаев получается противоречие с нашим предположением, что кратчайший путь из произвольного города Х в произвольный город Y проходит через n > 2 городов. Значит наше предположение неверно и из любого города в любой можно добраться с n <= 2 пересадками.