Решение задачи 198

Условие:

Прямая покрашена в два цвета. Докажите, что найдутся три одноцветные точки A, B и C такие, что точка B является серединой отрезка AC.

Решение:

Рассмотрим две точки одного цвета X и Y. Считаем, что они окрашены в белый цвет. Рассмотрим еще три точки P, O и Q такие, что О -- середина XY, X -- середина PY, Y -- середина XQ. Очевидно, что O -- середина PQ.

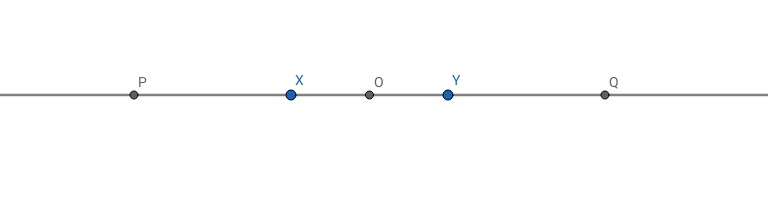
Если какая-нибудь из точек P, O, Q окрашена в белый цвет, то она вместе с точками X, Y образует искомую тройку. Если же все точки P, O, Q черные, то они образуют искомую тройку.

Источник: Книга "В.О.Бугаенко. Турниры им. Ломоносова. Конкурсы по математике. МЦНМО-ЧеРо. 1998".