Решение задачи 180

Условие:

По основанию равнобедренного треугольника движется точка. Докажите, что сумма расстояний от нее до боковых сторон не меняется.

Решение:

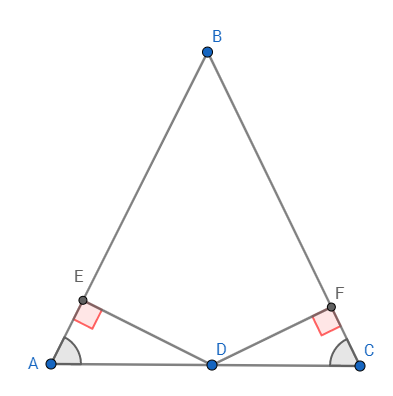
Пусть дан равнобедренный треугольник ABC, AB=BC, AC -- основание. Пусть точка D лежит на основании. Пусть точки E и F -- основания высот, опущенных из точки D на стороны AB и BC соответственно.

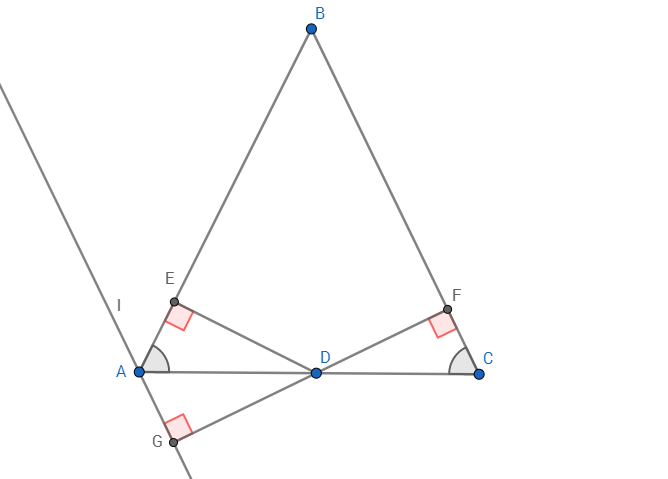
Проведем через точку A прямую, параллельную BC. Обозначим ее через l. На эту прямую из точки D опустим перпендикуляр. Основание это перпендикуляра обозначим через G.

Так как прямые AG и BC параллельны, то накрест лежащие углы С и DAG равны. Далее, ∠EDA=∠FDC=∠ADG, так как они все равны 180-90-α, где α=∠C=∠A=∠DAG.

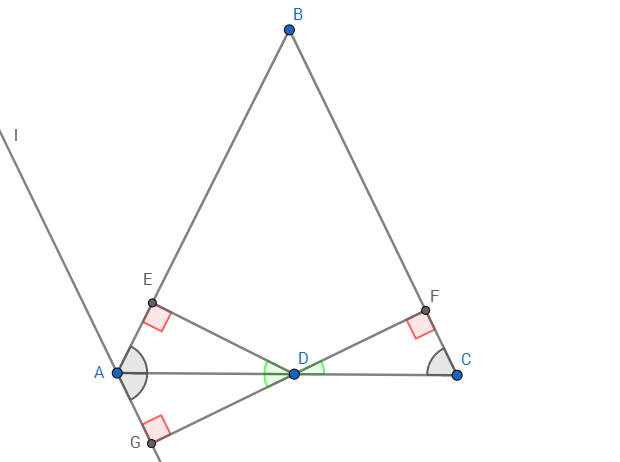
Треугольники EDA и ADG равны по трем углам и общей гипотенузе, значит DE=DG. Из равенства углов ADG и FDC следует, что точки G, D и F лежат на одной прямой. Получается, DE+DF = DG+DF = GF, то есть сумма расстояний до боковых сторон от точки D равно расстоянию между двумя фиксированными параллельными прямыми, которое никак не зависит от выбора точки D.