Решение задачи 171

Условие:

На отрезке длиной 1 расположено несколько отрезков, полностью его покрывающих. Докажите, что можно выбросить некоторые из них так, чтобы оставшиеся по-прежнему покрывали отрезок и сумма их длин была меньше 2.

Решение:

Без ограничения общности считаем, что отрезок длиной 1 это отрезок [0;1]. Среди отрезков содержащих точку 0 рассмотрите тот, у которого правый конец лежит правее других (он может быть не один). Обозначим его правый конец через x₁, а сам отрезок назовем первым.

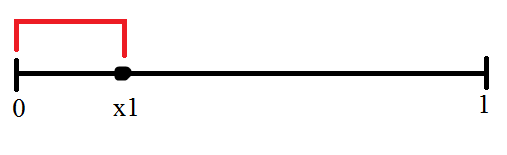
Далее среди отрезков, содержащих точку x₁ рассмотрим тот, у которого правый конец лежит правее других. Обозначим его правый конец через x₂, а сам отрезок назовем вторым.

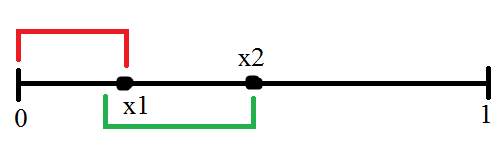
Аналогично первым двум отрезкам найдем третий отрезок.

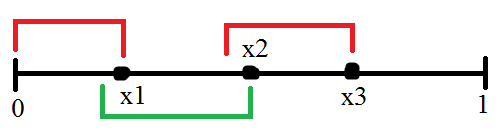
Нетрудно видеть, что третий отрезок не содержит точку x₁. Действительно, если бы третий отрезок содержал точку x₁, то на втором этапе мы бы взял его, так как у третьего отрезка правый конец правее, чем у второго, но второй отрезок выбран так, что у всех других отрезков содержащих точку x₁, правый конец находится не правее чем у него. Отсюда делаем вывод, что первый и третий отрезки не пересекаются. Далее продолжаем строить цепочку отрезков (на каждом этапе берем отрезок с самым правым концом, содержащий правый конец предыдущего отрезка). Тогда отрезки с нечетными номерами не пересекаются (они сверху на картинке) и отрезки с четными номерами не пересекаются (они снизу на картинке).

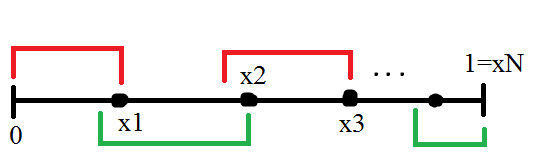
Получается, что мы покрыли отрезок [0;1]. Заметим, что общая длина отрезков с нечетными номерами (верхних/красных) меньше 1 (т.к. они попарно не пересекаются). Также общая длина отрезков с четными номерами (нижних/зеленых) меньше 1. Значит общая длина всех отрезков меньше 2.