Решение задачи 154

Условие:

Докажите, что среди любых шести человек найдутся либо трое попарно знакомых, либо трое попарно незнакомых.

Решение:

Как уже говорилось в подсказке, считаем, что люди - вершины графа. Ребра есть двух цветов - красные и синие. Между двумя людьми (вершинами) проведено красное ребро, если они знакомы и синее в противном случае. Тогда условие задачи можно переформулировать следующим образом: Докажите, что в полном графе (в котором из каждой вершины в каждую проведено ребро) на 6 вершинах, рёбра которого покрашены в 2 цвета, всегда найдётся одноцветный треугольник.

Рассмотрим произвольную вершину ("звёздочка"). Из нее выходят 5 двухцветных рёбер во все остальные вершины. Согласно принципу Дирихле, мы можем утверждать, что существует по крайней мере 3 одноцветных ребра, выходящих из вершины "звёздочка" (есть 2 цвета и 5 рёбер, тогда найдется по крайней мере 3 одноцветных ребра).

Без ограничения общности будем считать, что из "звёздочки" выходит 3 красных ребра в вершины "1","2" и "3":

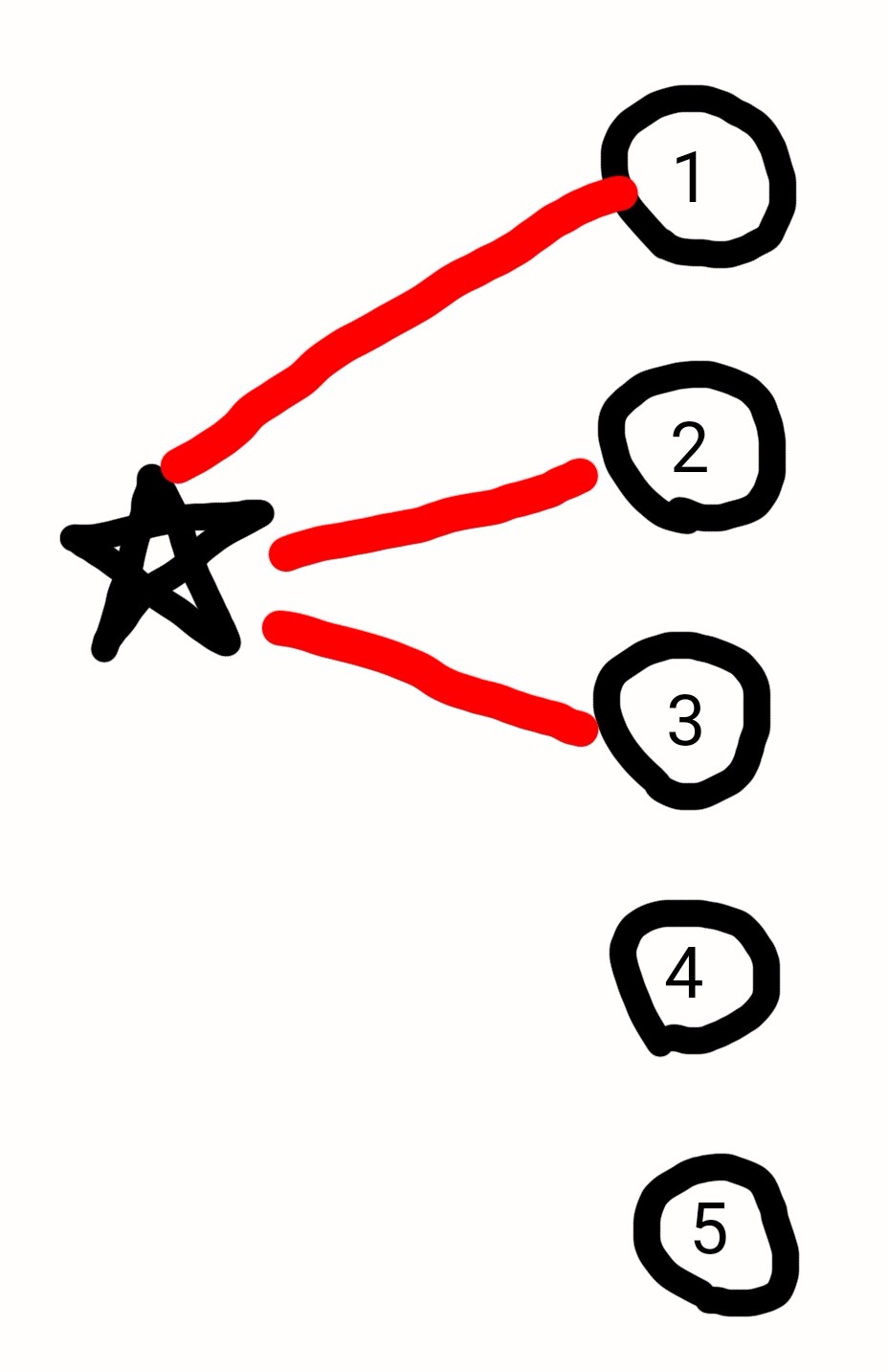
Рассмотрим эти три вершины "1","2" и "3". Если какие-то две из них соединены красным ребром, то красный треугольник нашёлся (эти две вершины и "звёздочка"):

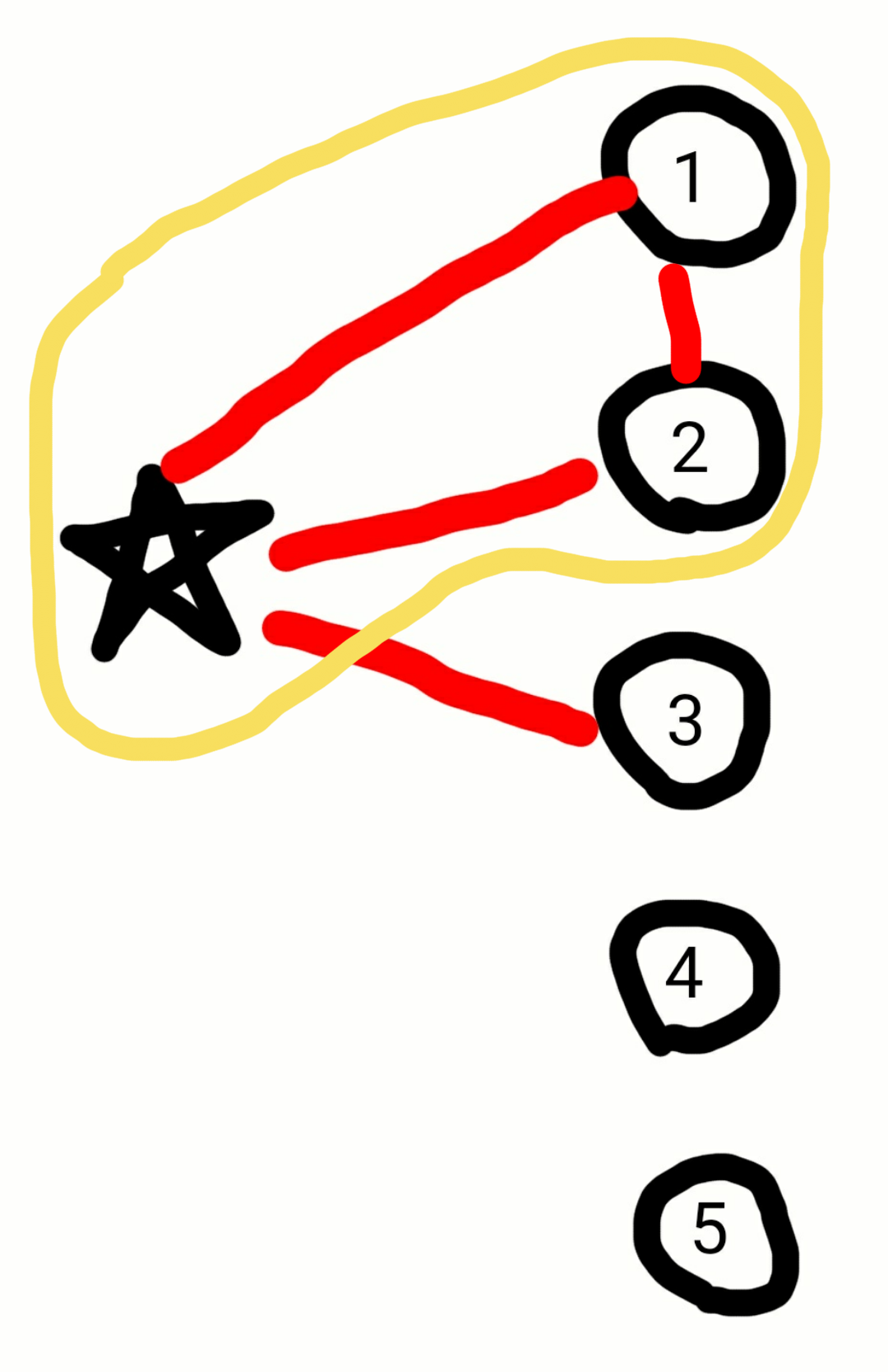
В противном случае, когда среди рёбер на этих трёх вершинах нет красных, мы получаем синий треугольник:

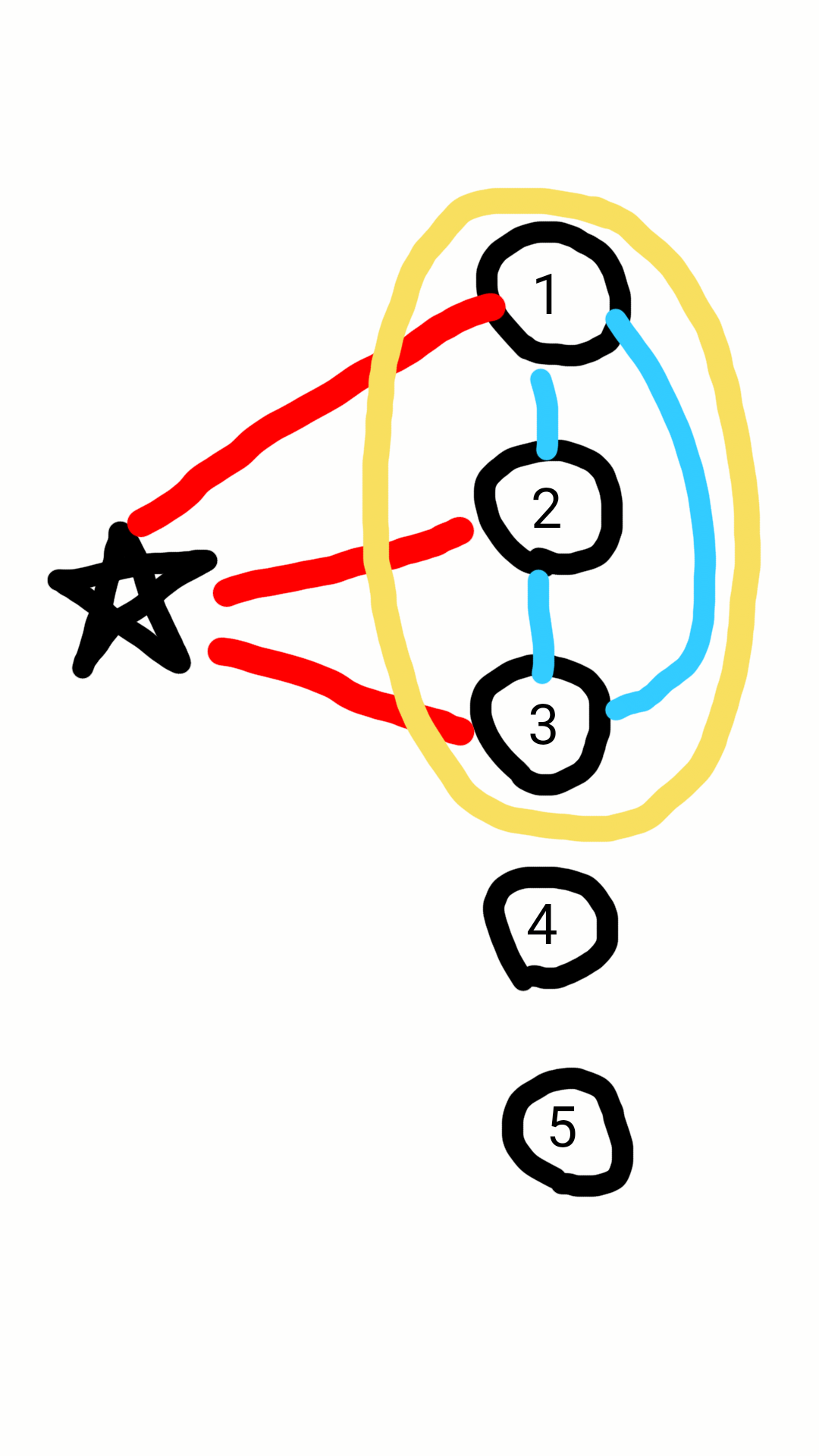
Как мы видим, в любом случае существует одноцветный треугольник, что и решает нашу задачу!