Д-во Т. о 3-х колпаках

Напомню формулировку:

Теорема о 3-х колпаках: Точки O_i — центры внешних гомотетий 3-х данных окружностей, точки I_i — центры внутренних.

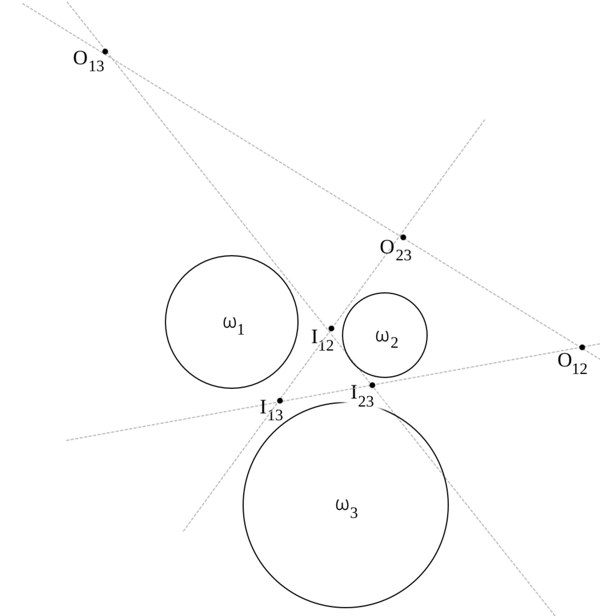
Нужно доказать, что точки:

1) O_13, O_12, O_23

2) O_13, I_12, I_23

3) I_13, O_12, I_23

4) I_13, I_12, O_23

лежат на одной прямой.

Доказательство:

Для начала проведем док-во для внешних центров гомотетий.

Выйдем в 3D. Достроим над центрами данных окружностей точки U_1, U_2 и U_3 так, чтобы U_i были на высоте r_i, где r_i — радиус ω_i.

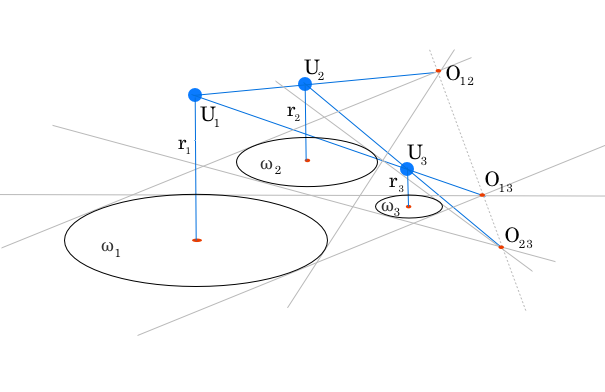
Лемма: U_iU_j проходит через O_ij.

□ При гомотетии с центром в точке O_ij точка U_i переходит в U_j, так как окружность ω_i переходит в ω_j ■

Рассмотрим плоскость, проходящую через точки U_1, U_2 и U_3. Ее прямая пересечения с исходной плоскостью содержит точки O_1, O_2 и O_3. Значит, O_i лежат на одной прямой.

Доказательство того, что, например, O_13, I_12, I_23 лежат на одной прямой, аналогично. Но в этом случае точку U_2 нужно достраивать не вверх, а вниз.